Programmation:OCaml:Modules

Introduction

Lorsque la taille des programmes augmente, il devient nécessaire d'introduire une organisation et un découpage de ceux-ci. De l'approche la plus simple qui consiste à regrouper les différents fichiers source du programme au moment de la compilation, jusqu'au mécannisme de programmation générique les plus évolués comme les foncteurs, tous les langages de programmation proposent des solutions pour découper le code.

Mais la programmation modulaire n'est pas juste une affaire de ranger son code dans des fichiers séparés. L'objectif est de structurer et d'organiser pour minimiser les redondances, factoriser les constructions du langage et améliorer l'accessibilité (notamment pour les opérations de maintenance.)

Une partie des notions vues dans ce cours ne sont pas limitées à OCaml, bien que celui-ci soit notre langage d'application.

Programmation modulaire

Avant de découvrir les éléments spécifiques à OCaml, intéressons nous aux notions génériques. La programmation modulaire s'appuie tant sur la conception que sur la réalisation. Elle intervient donc très tôt dans le processus de développement d'un programme et à un impact sur tout le reste de la chaîne.

Découpage et compilation séparée

On appelle module (ou unité, ou ... ) une portion autonome d'un programme qui se trouve en règle générale dans un fichier séparé (ce n'est pas toujours le cas, il existe différent niveau de découpage, mais l'idée reste la même.) Cette portion peut être compilée séparément du reste du programme (c'est en ce sens qu'elle est autonome) et sera réintégrée plus tard (à la fin de la compilation via l'édition de lien, voir à l'exécution dans le cas des bibliothèques dynamiques.)

On utilise généralement les modules pour regrouper un ensemble de déclarations (fonctions, types, classes ... ) centrées sur le même thème. La plus part des mécannismes de module fournissent également la possibilité de différencier du code publique (visible de tous) et du code priver (uniquement accessible à l'intérieur du module.) Le cas d'école est la description d'une structure de données accompagnée de l'ensemble de ses opérations, en incluant le module, on récupérera tous les outils nécessaires à l'utilisation de cette structure, d'un autre côté, le module pourra abstraire l'implantation de la structure en nous cachant certains détails.

La compilation d'un programme découpé en module se déroule en règle générale toujours suivant le modèle ci-après:

1. Construction des dépendances entre modules (souvent réaliser par le programmeur, ou par un outil idoine, avant la compilation.)
2. Compilation des modules indépendement les un des autres (lors des recompilation, on pourra ne recompiler ici que le stricte nécessaire.)
3. Compilation du programme principal
4. Édition de lien: c'est ici que l'ensemble des éléments est regroupé en un tout final, votre programme.

La compilation des modules passe par la génération d'objet (les .o en C, les .cmo et .cmx en OCaml). Ces objets sont en général des portions de code binaire dont un certain nombre d'éléments sont irrésolus. L'édition de lien se charge de regrouper ces objets et de connecter les différentes références (appels de fonctions, constantes ... ) pour en faire un programme exécutable.

Organisation

Le principe de compilation séparée n'impose pas à priori, de méthodologie de découpage, ni d'organisation particulière, si ce n'est des problèmes de reconnaissance de symboles au moment de la compilation du module. Notre objectif est bien évidement d'aller un peu plus loin et de profiter du mécannisme de compilation séparée pour organiser et factoriser notre code.

Structures et types abstraits

Les modules les plus simples à découper concerne les structures des données: on regroupe dans un même module l'ensemble des opérations associées à une structure. C'est là que les types abstraits (au sens de Edsger Dijkstra ou de Christophe Boullay) entre en jeux.

La définition d'une structure de données se fait sur deux niveaux:

• l'exploitation: comment utilisons nous cette structure, via quelles opérations.
• l'implantation: comment la structure est effectivement représentée en mémoire et le code des opérations correspondantes.

On va retrouver cette logique dans la construction des modules: l'interface du module (la partie publique) définira l'exploitation et le code du module définira l'implantation.

Lorsque l'on commence à découper un projet, on isole les structures essentielles (celles qui ne dépendent d'aucune autre) et on les place chaqu'une dans son module. On recommence ensuite pour les autres structures par vagues successives (on définit le module lorsque touts les prérequis le sont.)

Entités logiques et activités

Une fois les structures de données isolées, il faut ranger le reste du code. Là encore, il s'agit simplement de logique: lorsque les activités du programme ont été identifiées, on regroupe dans un même module l'ensemble du code nécessaire à chaque activité.

L'opération est incrémentale, comme pour les structures de données, on s'intéresse d'abord aux activités les plus autonomes et on progresse vers les activités les plus gobales par regroupements successifs.

Interfaces

Une fois le découpage logique effectué, il faut mettre en place l'interface des modules. Cette phase, qui fait encore partie de la conception, est importante à la fois pour la réalisation finale mais également pour le découpage et la répartition du travail.

Une fois chaque module identifié, il faut établir l'ensemble des symboles (types, fonctions ... ) fournit par le module. Cette définition peut se faire de manière informelle (du moment que les informations nécessaires sont là) ou directement sous forme d'interface des modules dans votre langage de programmation (en l'occurrence le fichier .mli en OCaml ou le fichier .h.)

Pour établir l'interface de votre module vous avez globalement deux approches: interne ou externe. Soit vous décidez de décrire le module directement par ses opérations, auquel cas l'interface du module correspond directement à cette description. Soit, vous optez pour la logique inverse: là (conceptuellement parlant) où vous utilisez votre module, vous établissez les opérations dont vous avez besoin.

La seconde approche, qui pourrait paraître bizarre, est probablement la plus sûre: toutes les opérations nécessaires (et seules celles qui sont nécessaires) vont émerger de cette phase de conception, évitant l'oubli d'opération ou la réalisation de code inutile. Cette approche fera probablement aussi émerger certains aspects de l'utilisation du module qui pourrait orienter son implantation. Par exemple, si l'on considère un module décrivant une table associative, si à l'utilisation les opérations qui s'avèrent importantes sont l'ajout, la suppression bien imbriqués (voir le cours sur les structures de données) et de manière générale une utilisation fonctionnelle de la structure, le choix d'implantation se portera plus naturellement vers des AVL que vers des tables de hachages.

Dépendances

Une fois le découpage (voir pendant le découpage) en module, il faut définir les dépendances entre modules. Un module A dépend d'un autre module B, lorsque A utilise des opérations de B.

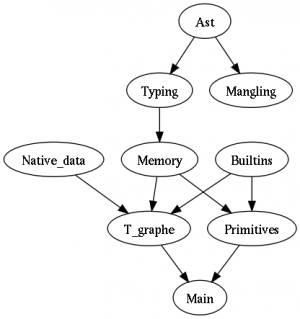
La méthode la plus simple travailler avec les dépendances est de construire un graphe de dépendances (voir la figure.) Dans un tel graphe, il existe un arc (une flêche) d'un module A vers un module B si B dépend A.

Graphe de dépendances

Le graphe de dépendances doit être sans cycle pour être valide. La présence de cycle indique souvent des erreurs de conceptions ou un mauvais découpage. En règle générale, lorsqu'il y a des dépendances circulaires (présence de cycle), c'est que l'un des modules définit des opérations qui devraient indépendantes, dans ce cas là déplacer les opérations fautives dans une nouveau module devrait suffir pour régler le problème.

Mais certains cas de dépendances circulaires ne sont pas forcément solubles en créant des modules supplémentaires. Il est parfois nécessaire de conserver une apparente circularité (interraction entre algorithme et structures de données, modélisation vue/moteur ... ), dans ce cas, nous utiliserons les outils de généricités mis à notre disposition: polymorphisme, ordre supérieur, objets et interfaces, functeurs ...

En OCaml, le graphe de dépendances permettra également d'établir un ordre pour les modules sur la ligne de compilation.

Les dépendances sont également important dans la construction d'un Makefile. En effet, make (et les outils du même genre) compile un projet en s'appuyant sur les informations de dépendances pour construire les fichiers dans l'ordre et ne recompiler que le stricte nécessaire à chaque fois.

Certains outils sont capables d'établir (plus ou moins bien) les dépendances entre modules automatiquements: ocamldep, makedepend, gcc -M ...

Les modules dans OCaml

OCaml fournit une sous-langage complet pour utiliser les modules. Ce sous-langage permet non seulement de séparer le code en fichier séparés, mais également de construire des modules imbriqués et des foncteurs.

Syntaxe

Les noms de module sont des identifiants particulier, qui répondent aux mêmes contraintes que les constructeurs de type somme ou les exceptions: le premier caractère est forcément une lettre majuscule, et le reste de l'identifiant doit être un caractère alphanumérique ou un underscore (_).

On retrouve le nom des modules dans trois contextes:

• Lors d'une référence direct à un symbole du module sous la forme: A.x (où A est le nom du module et x un des ses symboles publiques.)
• Lors d'une ouverture de l'espace de nommage avec la directive open: open A rend tous les symboles publiques du module A directement accessible sans les préfixés par A.
• Dans le nom du fichier du module: le module MonModule doit se trouver (s'il n'est pas imbriqué) dans le fichier monModule.ml.

Tout symbole définit par un let, tout type ou toute exception déclaré dans le module sera visible par défaut (pour cacher certaines définitions il faudra faire une interface.)

Voici par exemple un module Vector (donc sauver dans le fichier vector.ml) qui définit un type vect et les opérations associées:

(* module Vector *)
 
exception Vector_full
exception Index_out of int
 
type 'a vect =
{
  mutable size : int;
  tab : 'a array;
}
 
let make max base =
  {
    size = 0;
    tab = Array.make max base;
  }
 
let len v = v.size
 
let add x v =
  if v.size < Array.length (v.tab) then
    begin
      v.tab.(v.size) <- x;
      v.size <- v.size + 1
    end
  else raise Vector_full
 
let get i v =
  if i < v.size then
    v.tab.(i)
  else
    raise (Index_out i)
 
let insert x i v =
  if i < v.size then
    if v.size < Array.length v.tab then
      begin
	for j = v.size downto i+1 do
	  v.tab.(j) <- v.tab.(j-1)
	done;
	v.tab.(i) <- x;
	v.size <- v.size + 1
      end
    else raise Vector_full
  else raise (Index_out i)
 
let print to_s v =
  let s = ref "|" in
    for i = 0 to v.size - 1 do
      s := !s ^ " " ^ (to_s v.tab.(i)) ^ " |"
    done;
    let l = (String.make (String.length !s) '-') in
      Printf.printf "%s\n%s\n%s\n" l !s l;

Le programme suivant utilise les vecteurs du module Vector que nous venons de définir:

(* exampleModule.ml *)
 
let remplissage n =
  let v = Vector.make n 0 in
    for i = 0 to n-1 do
      Vector.add i v
    done;
    v
 
let main () =
  begin
    if Array.length Sys.argv > 1 then
      let v = remplissage (int_of_string Sys.argv.(1)) in
	begin
	  Vector.print string_of_int v;
	  (try Vector.add 42 v with
	       Vector.Vector_full ->
		 Printf.printf "Vecteur plein !\n");
	  exit 0;
	end
    else
      begin
	Printf.eprintf "usage: exampleModule <entier>\n";
	exit 1;
      end
  end
 
let _ = main ()

On pourrait le réécrire sous en utilisant open:

(* exampleModule.ml *)
 
open Vector
 
let remplissage n =
  let v = make n 0 in
    for i = 0 to n-1 do
      add i v
    done;
    v
 
let main () =
  begin
    if Array.length Sys.argv > 1 then
      let v = remplissage (int_of_string Sys.argv.(1)) in
	begin
	  print string_of_int v;
	  (try add 42 v with
	       Vector_full ->
		 Printf.printf "Vecteur plein !\n");
	  exit 0;
	end
    else
      begin
	Printf.eprintf "usage: exampleModule <entier>\n";
	exit 1;
      end
  end
 
let _ = main ()

Nous verrons un peu plus loin que la directive open est souvent source de confusion et d'ambiguïté et qu'il est plus simple de faire sans.

Compilation séparée

Pour compiler le programme suivant, il nous faut produire le code objet du module vecteur. En OCaml, il y a deux parties distinctes: l'interface et l'implantation. Dans notre cas, vu que nous n'avons défini aucune interface, les deux seront produits à partir du même fichier. Dans l'exemple, nous allons aussi séparé complètement l'étape d'édition de lien des étapes de compilation en compilant le fichier principal comme un module. Le déroulement de la compilation est le suivant:

> ocamlc -c vector.ml
> ocamlc -c exampleModule.ml
> ocamlc -o exampleModule vector.cmo exampleModule.cmo

Ou, en version native:

> ocamlopt -c vector.ml
> ocamlopt -c exampleModule.ml
> ocamlopt -o exampleModule vector.cmx exampleModule.cmx

La version suivante marche également:

> ocamlopt -c vector.ml
> ocamlopt -o exampleModule vector.cmx exampleModule.ml

On pourrait écrire un Makefile pour ce code:

# Makefile exampleModule
 
OCAMLC = ocamlc.opt
OCAMLOPT= ocamlopt.opt
 
exampleModule: vector.cmx exampleModule.cmx
	${OCAMLOPT} -o exampleModule vector.cmx exampleModule.cmx
 
exampleModule.cmx: exampleModule.ml vector.cmx
	${OCAMLOPT} -c exampleModule.ml
 
vector.cmx: vector.ml
	${OCAMLOPT} -c vector.ml
 
# END

On peut même automatiser un peu les choses:

# Makefile exampleModule
 
OCAMLC = ocamlc.opt
OCAMLOPT= ocamlopt.opt
 
exampleModule: vector.cmx exampleModule.cmx
	${OCAMLOPT} -o exampleModule vector.cmx exampleModule.cmx
 
exampleModule.cmx: vector.cmx
exampleModule.cmo: vector.cmo
 
# Règles génériques de compilation des modules:
 
.SUFFIXES: .ml .mli .cmo .cmx .cmi
 
.ml.cmo:
	${OCAMLC} -c $<
 
.ml.cmx:
	${OCAMLOPT} -c $<
 
.mli.cmi:
	${OCAMLC} -c $<
 
# Netoyage
 
clean::
	rm -f *~
	rm -f *.cm? *.o
	rm -f exampleModule
 
# END

Modules imbriqués

L'encapsulation de module ne s'arrête pas à la compilation séparée en OCaml. En effet, il est possible de définir des modules à l'intérieur des modules, on parle alors de modules imbriqués.

La syntaxe est la suivante:

module A =
struct
  type t = Int of int | Float of float
  let add x y = match (x,y) with
      (Int i1, Int i2) -> Int (i1 + i2)
    | (Float i1, Float i2) -> Float (i1 +. i2)
    | (Int i, Float f) | (Float f, Int i) ->
	Float (f +. float i)
  let compare x y = match (x,y) with
      (Int i1, Int i2) -> Pervasives.compare i1 i2
    | (Float f1, Float f2) -> Pervasives.compare f1 f2
    | (Int i, Float f) ->
	Pervasives.compare (float i) f
    | (Float f, Int i) ->
	Pervasives.compare f (float i)
end
 
let x = A.add (A.Int 42) (A.Float 0.)

La réponse d'OCaml (interpréteur) est la suivante:

module A :
  sig
    type t = Int of int | Float of float
    val add : t -> t -> t
    val compare : t -> t -> int
  end
val x : A.t = A.Float 42.

Comme le montre cet exemple, on peut définir un module à l'intérieur d'un fichier (qui par essence définit lui même un module.) Ce module s'utilise de la même manière que les autres, sauf qu'à l'extérieur du fichier où il est défini, il est un symbole publique comme les autres et doit être accédé de la même manière: si notre exemple précédant se trouve dans le fichier b.ml, alors on accèdera à la fonction add avec la notation B.A.add.

On peut définir un module à partir d'un autre (pour faire une sorte d'alias):

module BA3 = Bigarray.Array3

On pourra ainsi utiliser les symboles définis dans Bigarray.Array3 en utilisant le préfix BA3. Il est également possible de définir un module localement:

let s =
  let module BI = Big_int in
    BI.string_of_big_int (BI.power_int_positive_int 10 10000)

La définition locale de module peut s'utiliser pour sélectionner un module particulier dans certain contexte. Prennons un exemple simple: nous avons deux modules dont le rôle est d'afficher les messages d'erreurs de notre programme, l'un des modules affiche les messages en français l'autre en anglais. Les deux fournissent une unique opération print_err qui prend en paramètre une valeur indiquant l'erreur (définit dans un autre module.) Voici les différents fichiers de l'exemple:

(* module Arith *)
 
type error =
  | Unknown_err
  | Wrong_param of int * string
  | Div_zero of string
  | Unknown_op of string
  | Bad_params of string
 
exception Invalid_param of int * string
exception Div_by_zero of string
 
let fact n =
  if n<0 then raise (Invalid_param (n,"fact"))
  else
    let rec aux a = function
	0|1 -> a
      | n -> aux (a*n) (n-1)
    in
      aux 1 n
 
let pow a = function
    0 -> 1
  | b when b<0 -> raise (Invalid_param (b,"pow"))
  | b ->
      let rec qpow accu x = function
	  0 -> accu
	| y ->
	    qpow
	      (if y mod 2 = 0 then accu else (x * accu))
	      (x * x) (y lsr 1)
      in qpow 1 a b
 
let protected_div a b =
  if b=0 then raise (Div_by_zero "div")
  else a/b
 
let menu perror op params =
  try
    match (op,params) with
	("fact",x::[]) ->
	  Printf.printf "!%d = %d\n" x (fact x)
      | ("pow",[a;b]) ->
	  Printf.printf "%d ** %d = %d\n" a b (pow a b)
      | ("div",[a;b]) ->
	  Printf.printf "%d / %d = %d\n" a b (protected_div a b)
      | (("fact"|"pow"|"div"),_) -> perror (Bad_params op)
      | _ -> perror (Unknown_op op)
  with
      Invalid_param (n,o) -> perror (Wrong_param (n,o))
    | Div_by_zero o -> perror (Div_zero o)
    | _ -> perror Unknown_err

(* module Perror_fr *)
 
let perror_fr = function
    Arith.Unknown_err ->
      Printf.eprintf "Erreur inconnue\n"; exit 1
  | Arith.Wrong_param(n,op) ->
      Printf.eprintf "%s: %d est un mauvais paramètres\n" op n; exit 1
  | Arith.Div_zero op ->
      Printf.eprintf "%s: division par 0\n" op; exit 1
  | Arith.Unknown_op op ->
      Printf.eprintf "%s: opération inconnue\n" op; exit 1
  | Arith.Bad_params op ->
      Printf.eprintf "%s: nombre de paramètres incorrect\n" op; exit 1

(* module Perror_en *)
 
let perror_en = function
    Arith.Unknown_err ->
      Printf.eprintf "Unknown error\n"; exit 1
  | Arith.Wrong_param(n,op) ->
      Printf.eprintf "%s: wrong parameter value %d\n" op n; exit 1
  | Arith.Div_zero op ->
      Printf.eprintf "%s: division by 0\n" op; exit 1
  | Arith.Unknown_op op ->
      Printf.eprintf "%s: unknown operation\n" op; exit 1
  | Arith.Bad_params op ->
      Printf.eprintf "%s: too many or not enough parameters\n" op; exit 1

(* module Main *)
 
(* Default to english error messages *)
let lang_fr = ref false
 
let q = Queue.create ()
 
let annon s = Queue.push (int_of_string s) q
 
let rec make_list q =
  try
    let x = Queue.pop q in x :: make_list q
  with
      Queue.Empty -> []
 
let op = ref ""
 
let spec = Arg.align
  [
    ("-fr",Arg.Set lang_fr, " error messages in french");
    ("-op",Arg.Set_string op, " operation to perform (mandatory)")
  ]
 
let umsg = "Module example prog."
 
let main () =
  begin
    Arg.parse spec annon umsg;
    if !op = "" then
      begin
	Arg.usage spec umsg;
	exit 2
      end;
    let perror =
      if !lang_fr then
	let module P = Perror_fr in P.perror_fr
      else Perror_en.perror_en
    in
      Arith.menu perror !op (make_list q);
      exit 0;
  end
 
let _ = main ()

# Makefile
 
OCAMLC = ocamlc.opt
OCAMLOPT= ocamlopt.opt
 
arith: arith.cmx perror_fr.cmx perror_en.cmx main.cmx
	${OCAMLOPT} -o arith arith.cmx perror_fr.cmx perror_en.cmx main.cmx
 
# Dependances
arith.cmo:
arith.cmx:
main.cmo: perror_fr.cmo perror_en.cmo arith.cmo
main.cmx: perror_fr.cmx perror_en.cmx arith.cmx
perror_en.cmo: arith.cmo
perror_en.cmx: arith.cmx
perror_fr.cmo: arith.cmo
perror_fr.cmx: arith.cmx
 
# Règles génériques de compilation des modules:
 
.SUFFIXES: .ml .mli .cmo .cmx .cmi
 
.ml.cmo:
	${OCAMLC} -c $<
 
.ml.cmx:
	${OCAMLOPT} -c $<
 
.mli.cmi:
	${OCAMLC} -c $<
 
# Netoyage
 
clean::
	rm -f *~
	rm -f *.cm? *.o
	rm -f arith
 
# END

Interfaces

On peut décrire un interface pour un module en OCaml, notamment pour restreindre les opérations visibles à l'extérieur du module. On emploit régulièrement le terme de signature pour parler des interfaces en OCaml, c'est un synonime.

Dans le cas d'un module défini par un fichier, il suffit de créer un fichier de même nom mais avec l'extension .mli. Dans ce fichier nous allons retrouver les définitions publiques du module sous la forme suivante:

• Pour tout symbole défini par un let symbole = ... dans le module, on utilisera val symbole : t (où t est le type de symbole.)
• Pour les définitions d'exception ou de type, on retrouvera les même définition avec la même syntaxe.

Prennons l'exemple du module suivant:

(* module A *)
 
(* fonction privee *)
let priv x = (x,x)
 
(* fonction publique *)
let pub x = (x,(x,x))

Son interface sera:

(* a.mli *)
 
val pub : 'a -> 'a * ('a * 'a)

Dans le cas d'un module imbriqué, il existe plusieur possibilité. On peut soit directement donné l'interface du module au moment de sa déclaration avec la syntaxe suivante:

module M :
sig
  type 'a t = Rien | Truc of 'a t
  val truc : 'a t -> 'a t
end =
struct
  type 'a t = Rien | Truc of 'a t
  let truc a = Truc a
  let rec bidule = function
      Rien -> ()
    | Truc a -> bidule a
end

On peut également définir un type de module (une interface qui n'est pa forcément attachée a un module) que l'on rattachera (ou pas) à la définition du module:

(* ex_interface.ml *)
module type IntType =
sig
  type t = int
  val compare : t -> t -> int
end
 
module Int : IntType =
struct
  type t = int
  let compare a b = a - b
end
 
module Int2 =
struct
  type t = int
  let divisible a b = a mod b = 0
 
  let compare a b =
    if divisible a b then -1
    else
      if divisible b a then 1
      else 0
end
 
module Int3 : IntType = Int2

Regardons l'évaluation de ces définitions:

module type IntType = sig type t = int val compare : t -> t -> int end
module Int : IntType
module Int2 :
  sig
    type t = int
    val divisible : int -> int -> bool
    val compare : int -> int -> int
  end
module Int3 : IntType

Génération automatique de signatures

Bien qu'en théorie il faille écrire la signature des modules avant de les écrire eux mêmes (vous êtes censés avoir préparer le découpage de votre programme avant de l'avoir codé), on peut parfois avoir besoin d'engendrer l'interface d'un module. Pour ça OCaml fourni un option -i sur ses deux compilateurs qui permet de réaliser la phase de typage et d'afficher sur la sortie standard ce qu'il aurait fallu mettre dans le .mli (pour avoir tout publique.) Regardons sur quelques examples:

(* module Truc *)
 
let rec fact = function
    0|1 -> 1
  | n -> n * fact (n-1)
 
let rec intfold f a = function
    0 -> a
  | n -> intfold f (f a n) (n-1)

> ocamlc -i truc.ml
val fact : int -> int
val intfold : ('a -> int -> 'a) -> 'a -> int -> 'a
>

Type opaque

On veut parfois cacher l'implantation d'un type et ne laisser visible que les opérations qui l'utilisent. Dans ce cas, il suffit de ne pas donner la définition explicite du type dans l'interface du module. Voici un petit exemple (en utilisant un module imbriqué):

module Pile :
sig
  exception Pile_vide
  type 'a t
  val push : 'a -> 'a t -> 'a t
  val pop  : 'a t -> 'a * 'a t
  val is_empty : 'a t -> bool
end =
struct
  exception Pile_vide
  type 'a t = 'a list
  let push x p = x::p
  let pop = function
      [] -> raise Pile_vide
    | h::t -> (h,t)
  let is_empty = function
      [] -> true | _ -> false
end

On peut également utiliser cette notion pour vérifier (ou forcer) le typage d'un module particulier. Supposons que vous aillez un type de module Comparable qui décrive le fait que le module définit un type t et une fonction de comparaison. Le type t doit être générique et donc opaque. Ainsi, vous pourrez forcer la un module (fournissant les bonnes définitions) à avoir cette signature. Voici un petit exemple:

module type Comparable =
sig
  type t
  val compare: t -> t -> int
end
 
module CompInt : Comparable =
struct
  type t = int
  let compare a b = a - b
end
 
(*
 * Le module String d'OCaml fourni un type t et une fonction de
 * comparaison.
 *)
module CompString : Comparable = String

Convention de nom

L'accès aux symboles d'un module sous la forme A.symb permet également de mettre en place un système d'espace de nom (namespace.) Comme les modules décrivent souvent des structures de données, il n'est pas rare qu'il est des conflits entre les noms de opérations. Si l'on considère, par exemple, une série de module décrivant des collections (structures de données servant à regrouper un ensemble de valeurs), il est fort probablement que chaque collection fournisse une opération d'ajout, un test du vide ou un accès à la taille ainsi que des itérateurs classiques.

Si les noms de vos opérations sont logiques, vous allez avoir des conflits de nom entre vos modules (pensez aux fonctions length des modules String, List ou Array.)

Avec des langages ne disposant pas d'un système de namespace, vous devez différentier explicitement toutes ces opérations (en général on prend une convention comme mettre en préfix ou suffix le nom du type sur lequel porte l'opération.) Au final, on se retrouve avec des noms relativement longs (aller regarder les opérations concernant les threads POSIX: pthread_cond_init, pthread_mutexattr_init, ou pthread_rwlockattr_init.)

La notation pointée, comme tous les système de namespace, nous propose une autre solution: par nature, les opérations seront préfixée par le nom de leur module. Ainsi, si vous regardez la bibliothèque standard d'OCaml, vous trouverez 13 fonctions length dans les différents modules (et même parfois dans des modules imbriqués dans le même module. C'est pourquoi il est fortement déconseillé d'utiliser la directive open.

La pratique la plus classique est de nommer les modules d'après le type qu'il définissent (c'est ce qui est fait dans la bibliothèque OCaml.) En règle générale, même le nom du type se limite à t, le nom du module étant suffisant.

Par exemple, définissons un module avec des arbres binaires standards:

(* module BinTree *)
 
type 'a t =
    Empty
  | Node of 'a t * 'a * 'a t
 
let empty () = Empty
 
let is_empty t = t = Empty
 
let rec size = function
    Empty -> 0
  | Node(ls,_,rs) ->
      1 + (size ls) + (size rs)
 
let rec height = function
    Empty -> -1
  | Node(ls,_,rs) ->
      1 + max (height ls) (height rs)
 
let rec add x = function
    Empty -> Node(Empty,x,Empty)
  | Node(ls,k,rs) ->
      if (size rs < size ls) then
	Node(ls,k,add x rs)
      else
	Node(add x ls,k,rs)
 
let rec mem x = function
    Empty -> false
  | Node(ls,k,rs) ->
      k=x || mem x ls || mem x rs

Voici maintenant un module pour les arbres généraux:

(* module GenTree *)
 
type 'a t =
  | Node of 'a * 'a t list
 
let make a = Node (a,[])
 
let rec size = function
    Node(_,l) ->
      List.fold_left (fun x t -> x + size t) 1 l
 
let rec height = function
    Node(_,l) ->
      List.fold_left (fun x t -> max x (height t)) 0 l
 
let rec add x = function
    Node (k,[]) ->
      Node(k,Node(x,[]))
  | Node(k,s::sons) ->
      Node(k,add x s::sons)
 
let rec mem x = function
    Node(k,sons) ->
      k=x || List.exists (mem x) sons

On peut maintenant manipuler les arbres binaires ou généraux dans le programme sans conflit de noms:

let rec grow add accu = function
    0 -> accu
  | n -> grow add (add n accu) (n-1)
 
let main () =
  begin
    let tb = grow BinTree.add (BinTree.empty ()) 42 in
    let tg = grow GenTree.add (GenTree.make 1) 41 in
      Printf.printf "size tb = %d\nsize tg = %d\n" (BinTree.size tb)
	(GenTree.size tg);
      exit 0
  end
 
let _ = main ()

Conclusion

Cours	Partie
Cours de Programmation EPITA/spé	Programmation:OCaml