Programmation:OCaml:Foncteurs

Introduction

La programmation modulaire est un premier pas vers une approche plus générique de la programmation. En effet, si vous implantez des structures de données usuelles sous forme de module, vous pourrez réutiliser facilement ces modules à différents endroits de votre programme, voir dans d'autre programme. Combiné avec le polymorphisme, vous pouvez construire des structures de données complètement génériques. Un bon exemple de cette possibilité est le module List qui fournit tout ce que vous pouvez vouloir sur les listes sans être limités à un type de listes particulier.

Pourtant, il existe des cas qui ne sont pas bien couvert par cette approche. En effet, supposons que vous vouliez implanter un structure de recherche triée (comme des AVL) mais dont la relation d'ordre n'est pas forcément l'ordre naturelle des valeurs OCaml. Pour atteindre construire un module vraiment générique il faut que toutes les opérations prennent en paramètre la fonction de comparaison de vos éléments. Le résultat est un peu lourd à l'utilisation et ne protège pas d'erreur de manipulation (que se passe-t-il si vous n'utilisez pas systématiquement la bonne fonction de comparaison ?)

Ce que l'on voudrait pouvoir faire ici, c'est définir un module qui utilise un autre module inconnu (c'est à dire dont on ne connait que la signature.) On peut simuler ce genre de comportement avec une définition du genre:

module type Comparable =
sig
  type t
  val compare: t -> t -> int
end
 
module T:Comparable = String
 
module OrderedImpList :
sig
  exception Empty
  type content = T.t
  type t
  val push : content -> t -> unit
  val pop : t -> content
  val is_empty : t -> bool
  val empty : unit -> t
end =
struct
  exception Empty
  type content = T.t
  type t = content list ref
  let elem_comp = T.compare
 
  let rec insert x = function
      [] -> x::[]
    | h::t as l when elem_comp x h < 0 -> x::l
    | h::t -> h::insert x t
 
  let push x s = s := insert x !s
 
  let pop s = match !s with
      [] -> raise Empty
    | h::t -> s := t; h
 
  let is_empty s = !s = []
 
  let empty () = ref []
end

Il suffit maintenant de remplacer la définition du module T si on veut utiliser nos listes ordonnées avec un autre type.

On aimerait que cette manipulation soit plus simple et un peu plus automatiser (pour l'instant il faut modifier un fichier, ce n'est pas exactement idéal pour distribuer un module générique ... ) C'est exactement le rôle des foncteurs !

Fonction sur les modules

Un foncteur est un module paramétré: il fait référence à un module dont seule la signature a été définie. Reprennons notre exemple précédant mais cette fois-ci à la sauce foncteur:

module type Comparable =
sig
  type t
  val compare: t -> t -> int
end
 
module OrderedImpList (T : Comparable) =
struct
  exception Empty
  type content = T.t
  type t = content list ref
  let elem_comp = T.compare
 
  let rec insert x = function
      [] -> x::[]
    | h::t as l when elem_comp x h < 0 -> x::l
    | h::t -> h::insert x t
 
  let push x s = s := insert x !s
 
  let pop s = match !s with
      [] -> raise Empty
    | h::t -> s := t; h
 
  let is_empty s = !s = []
 
  let empty () = ref []
end

Comme on le voit, pas beaucoup de surprise, le module est presque identique à l'original, la seule différence étant la définition où T est un paramètre (typé) et non plus un module existant.

Il existe deux syntaxes, comme pour les fonctions, celle que nous vennons de voir (qui est la version courte) et la syntaxe longue:

module OrderedBox = functor (T:Comparable) ->
struct
  type content = T.t
  type t = Box of content
  let get (Box x) = x
end

De cette manière on peut indiquer la signature du foncteur (afin par exemple de forcer le type de certaines opérations.)

module type OrderedBoxType = functor (T : Comparable) ->
sig
  type content = T.t
  type t
  val box : content -> t
  val get : t -> content
end
 
module OrderedBox : OrderedBoxType = functor (T:Comparable) ->
struct
  type content = T.t
  type t = Box of content
  let box x = Box x
  let get (Box x) = x
end

Types abstraits et foncteurs

Forcer la signature de cette manière ne pose pas de problème, mais on pourrait souhaiter respecter une signature plus générique qui ne décrit pas un foncteur. Dans ce cas là, nous sommes obligés de rendre abstrait le type content, puisque celui-ci est défini par rapport au module T. Dans ce cas là, on obtient le résultat suivant:

module type AbstractOrderedBoxType =
sig
  type content
  type t
  val box : content -> t
  val get : t -> content
end
 
module AbstractOrderedBox = (OrderedBox : (functor (T:Comparable) -> AbstractOrderedBoxType))

Mais attention, dans ce cas, le type content est opaque. Du coup, il n'est plus vraiment possible d'utilier le module:

module StringBox = AbstractOrderedBox(String)
let b = StringBox.box "foo"

L'évaluation va nous signaler l'erreur suivante:

let b = StringBox.box "foo";;
                      ^^^^^
Error: This expression has type string but an expression was expected of type
         StringBox.content = AbstractOrderedBox(String).content

Qui est assez logique, le type StringBox.content est opaque par conséquent, à l'extérieur du module, on ne connait pas sa nature réelle et il n'est donc pas possible de construire des valeurs de ce type.

Heureusement, il existe une solution pour spécifier le type abstrait au moment où on le connaît:

module AbstractOrderedBox =
  (OrderedBox :
     (functor (T:Comparable) ->
	AbstractOrderedBoxType with type content = T.t
     )
  )

L'exemple précédent ne pose plus de problème (le module StringBox) de typage. La question ici est pourquoi faire ça ? En fait, on obtient une contrainte qui offre des garanties de typage suplémentaire sur les modules.

Prennons l'exemple suivant: on définit un foncteur de listes ordonnées faisant office d'ensemble:

module type SET =
sig
  type content
  type t
  val empty : t
  val add : content -> t -> t
  val mem : content -> t -> bool
end
 
module Set :
  (functor (T:Comparable) ->
     SET with type content = T.t) = functor (T:Comparable) ->
struct
  type content = T.t
  type t = content list
  let empty = []
  let rec add x = function
      [] -> [x]
    | h::t as l when T.compare x h = 0 -> l
    | h::t as l when T.compare x h < 0 -> x::l
    | h::t -> h::add x t
  let rec mem x = function
      [] -> false
    | h::t -> (T.compare x h = 0) || (T.compare x h > 0 && mem x t)
end

Nous utilisons ici le principe d'interface avec type opaque décrit plus haut. Quel est le problème ? Il est simple, les fonctions d'ajouts (add) et d'appartenance (mem) reposent toutes les deux sur la pré-condition que la liste est triée à l'aide de la fonction de comparaison du module paramètre du foncteur.

La contrainte ici est double:

• les opérations ne peuvent avoir lieu que sur des éléments du type Set(T).t et donc ne peuvent pas travaillé avec des listes construites à la main.
• les éléments de type Set(T').t avec T' définissant le même type t que T mais une fonction de comparaison différente, ne sont pas compatible avec ceux de type Set(T).t.

Sans type opaque, il serait possible d'utiliser les opérations sur des listes ne vérifiant pas la pré-condition, conduisant à des résultats dangereux.

Généricité et utilisation

Concrètement à quoi servent les foncteurs ?

De nombreux conteneurs resposent sur l'existence d'opérations particulières portant sur les éléments contenus. Il existe de nombreux cas où des opérations génériques sont suffisantes, comme par exemple la comparaison polymorphique d'OCaml (Pervasives.compare), mais ce n'est pas toujours le cas (toujours dans les comparaisons, pour certains types construits on pourrait vouloir un ordre lexicographique différent de celui d'OCaml.)

On peut pallier au problème de l'existence d'opérations spécifiques en utilisant l'ordre supérieur (l'opération requise est passée en paramètre) mais là encore cette solution n'est pas toujours satisfaisante.

Prennons l'exemple d'une collection ordonnées (ici des ensembles sous forme de listes):

module OrderedSet =
struct
  type 'a t = 'a list
 
  let rec add comp x = function
      [] -> x::[]
    | h::t as l when comp x h = 0 -> l
    | h::t as l when comp x h < 0 -> x::l
    | h::t -> h::add comp x t
 
  let rec mem comp x = function
      [] -> false
    | h::t -> (comp x h = 0) || (comp x h < 0 && mem comp x t)
end

Les opérations add et mem n'ont de sens que si la liste passée en paramètre est triée suivant l'ordre défini par la même fonction comp que celle passée en paramètre.

L'utilisation d'un foncteur garantie ici que la même fonction de comparaison sera utilisée par tout sans pour autant dépendre d'une fonction prédéfinie.

Usage classique

Généralement, un foncteur se présente sous la forme suivante:

(* module MyCollection *)
 
(* Signature pour le paramètre du foncteur: *)
module type ContentType =
sig
  type t
  (* operations necessaires ... *)
end
 
(* Signature des instances du foncteur: *)
module type MyCollectionType =
sig
  type content
  type t
  (* operations ... *)
end
 
(* Le foncteur: *)
module Make :
  (functor (T:ContentType) ->
      MyCollectionType with type content = T.t) = functor (T:ContentType) ->
struct
  type content = T.t
  type t = (* ... *)
  (* operations ... *)
end

La signature de module ContentType correspond au module décrivant le contenu, la signature MyCollectionType correspond à la signature des instances du foncteur (pour pouvoir utiliser des types opaques) et enfin, le foncteur à proprement parler sera le module Make.

Exemple

On va construire un module de calcule arithmétique générique. L'idée est qu'une bonne partie des fonctions arithmétiques classiques reposent juste sur l'existence de quelques opérations et du caractère énumérable de l'ensemble sur lequel portent ces opérations. Il est donc tout à fait raisonnable que la puissance entière ou la factorielle puissent s'écrire pour n'importe quel ensemble énumérable pourvu de la multiplication (et donc de l'addition) comme par exemple l'ensemble des matrices carrées (et ses sous-ensembles comme l'ensemble des matrices 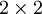$2\times 2$ ... )

On commence donc par définir une interface pour les modules comparables aux entiers (notez au passage les commentaires spéciaux pour ocamldoc):

module type Enumerable =
sig
  type t
    (** The type similar to integer *)
  val succ : t -> t
    (** The successor function *)
  val pred : t -> t
    (** The predecessor function *)
  val add : t -> t -> t
    (** The addition *)
  val mul : t -> t -> t
    (** The multiplication *)
  val compare : t -> t -> int
    (** The usual compare predicate for use with ordered collections. *)
end
(** The input signature of the functor {!GenArith.Make}. *)

On définit maintenant l'interface du résultat de l'application du foncteur:

module type S =
sig
  type t
    (** Inner representation of the type manipulated *)
  val power : t -> int -> t
    (** The integer generalized power function *)
  val fact : t -> t
    (** The generalized factorial function *)
end
(** The output signature of the functor {!GenArith.Make}. *)

On peut maintenant écrire le foncteur lui même:

module Make (T:Enumerable) : (S with type t = T.t) =
struct
  type t = T.t
 
  let p2 v = T.mul v v
 
  let rec power v = function
      0 -> T.one
    | 1 -> v
    | n ->
	T.mul
	  (if n mod 2 = 0 then T.one else v)
	  (power (p2 v) (n/2))
 
  let rec fact = function
      T.zero | T.one -> T.one
    | n -> T.mul n (fact (T.pred n))
 
end

On peut maintenant regrouper tout ça dans un seul fichier (que l'on nommera genArith.ml.) On pourra maintenant exploiter un module respectant l'interface Enumerable (ici des matrices carrées d'ordre 2 pourvue d'une relation d'énumération très simple.)

module Matrix : Enumerable =
struct
  type t = (int * int) * (int * int)
 
  let zero = ((0,0),(0,0))
  let one  = ((1,0),(0,1))
 
  let make a b c d = ((a,b),(c,d))
 
  let add ((a,b),(c,d)) ((a',b'),(c',d')) =
    ((a + a', b + b'),(c + c', d + d'))
 
  let mpred x = max 0 (x-1)
 
  let succ ((a,b),(c,d)) = ((a+1,b+1),(c+1,d+1))
  let pred ((a,b),(c,d)) =
    ((mpred a, mpred b),(mpred c, mpred d))
 
  let mul ((a,b),(c,d)) ((a',b'),(c',d')) =
    (
      (a * a' + b * c', a * b' + b * d'),
      (c * a' + d * c', c * b' + d * d')
    )
 
  let compare = Pervasives.compare
 
  let print ((a,b),(c,d)) =
    Printf.printf "| %4d %4d |\n" a b;
    Printf.printf "| %4d %4d |\n" c d;
end
 
module MatrixArith = Make(Matrix)

Les foncteurs de la bibliothèque standard

Un certain nombre de modules de la bibliothèque standard sont en réalité des foncteurs, c'est le cas des modules suivants:

• Map: tables associatives fonctielles (des AVL en pratique)
• Set: ensembles ordonnés
• MoreLabels.Map: version avec labels du module Map
• MoreLabels.Set: version avec labels du module Set

C'est quatre foncteurs reposent sur la même structure: une interface décrivant un type comparable (i.e. fournissant une fonction de comparaison) et un foncteur décrivant la structure de données. L'interface du type comparable est la suivante:

module type OrderedType =
sig
  type t
  val compare : t -> t -> int
end

Chaque fois le foncteur fourni s'appelle Make. De plus, ces modules fournissent également une interface décrivant les instances du foncteur (notamment pour rendre priver la représentation interne), cette interface s'appelle toujours S et est compatible avec l'interface OrderedType.

On trouve également d'autres modules qui fournissent une interface fonctorielle. C'est le cas du module Hashtbl qui définit des tables de hachage en s'appuyant sur la fonction de hachage générique d'OCaml mais permet aussi d'utiliser un foncteur prennant en paramètre un module qui fournira le test d'égalité et la fonction de hachage.

(* extrait de hashtbl.mli *)
 
module type HashedType =
sig
  type t
  val equal : t -> t -> bool
  val hash : t -> int
end

Cours	Partie
Cours de Programmation EPITA/spé	Programmation:OCaml