Programmation:OCaml:Bases

Introduction

Le langage OCaml (que vous avez découvert en SUP) est un langage fonctionnel, fortement typé, polymorphe et capable de faire de l'inférence de types. Ces un langage qui peut être aussi bien compilé qu'interprété. Bien que pure fonctionnel, il dispose de constructions impératives et d'un système d'objets. Il dispose également d'un sous-langage de modules où les modules sont des entités de premières classes.

Historiquement, Caml[1] était une implantation de la famille ML basé sur une machine abstraite à catégorie. Le passage en version Objective (le O de OCaml) a introduit un modèle de compilation en plusieurs passes permettant de produire du code pour des cibles matérielles et non plus seulement pour une machine abstraite. C'est également avec OCaml que les extensions qui différencie le langage des autres variantes de ML sont arrivées: objets, variants polymorphes, labels, foncteurs ...

OCaml est principalement un langage de recherche, il est développé à l'INRIA[2] et sert de laboratoire d'expérimentation pour les différentes avancées en théorie des langages (typage et sémantique.) Ce caractère expérimental n'en fait pas un bon outil pour le monde industriel, pourtant il est utilisé dans certains domaines principalement lorsque l'on a besoin de fiabilité sans pour autant perdre en performance. Le principal projet utilisant OCaml est Coq[3] un assistant de preuve (historiquement, Caml a été écrit pour écrire Coq) qui est l'un des rares systèmes de démonstration automatique à être reconnu par les mathématiciens. Coq est utilisé (en général) pour valider du logiciel critique, on peut citer par exemple l'implantation de la JavaCard de Schlumberger, certaines parties de TrustedBSD, Orange utilise aussi Coq dans ses centres de recherches pour la validation de protocoles.

Étant libre (avec sa propre licence), OCaml est également utilisé dans quelques logiciels libres, les plus connus sont Unison[4] (un File Synchronizer très puissant), MLDonkey[5] un client pour les réseaux peer-to-peer, Hevea[6] (un convertisseur LaTeX vers HTML), GeneWeb[7] (un outil de généalogie, visiblement très utilisé dans le milieu ... ), le code (en C) de la bibliothèque FFTW[8] est généré par un programme en OCaml, haXe[9] ("web oriented universal language"), Frama-c[10] (un outil d'analyse de programme C) et bien surement bien d'autres que vous pouvez trouver sur la bosse[11].

Les exemples donnés dans la suite du cours sont à tester par vous même pour mieux les comprendre. Les réponses d'OCaml ne sont pas données, c'est à vous de les déduire ou de les obtenir via l'interpréteur.

Le langage

OCaml est un dérivé de ML dont il reprend les grandes lignes en terme de syntaxe, de système de types et de sémantique. Étant un langage fonctionnel, on y manipule principalement des valeurs constantes (donc non modifiable) qui, en particulier, peuvent être des fonctions (on dit que le langage dispose de l'ordre supérieur, on encore que les fonctions sont des entités de premières classes.) Les 3 éléments clefs de syntaxe sont la déclaration de valeur (qui associe un nom au résultat d'une expression), l'abstraction qui permet de construire des fonctions et bien sûr l'application de fonction. Voici quelques petits exemples:

(* déclaration d'une valeur à partir d'une constante *)
let x = 1 ;;
 
(* déclaration d'une valeur à partir d'une expression *)
let x = 2 * 3 + 5 ;;
 
(* une valeur fonctionnelle *)
function x -> x + 1 ;;
 
(* appliquer une fonction *)
(function x -> x + 1) 1 ;;
 
(* Un petit mélange des trois ... *)
let f = function x -> x + 1;;
let x = f 1 ;;
let y = (f x) + f (f x) ;;
 
(* fonction à plusieurs arguments *)
let add = function x -> function y -> x + y ;;
let trois = add 1 2;;
 
(* Sucre syntaxique *)
 
(* Ces 3 fonctions sont équivalentes *)
let f = function x -> x + 1 ;;
let f = fun x -> x + 1 ;;
let f x = x + 1 ;;
 
(* Ces 3 fonctions sont aussi équivalentes *)
let add = function x -> function y -> x + y ;;
let add = fun x y -> x + y ;;
let add x y = x + y ;;

Le langage fournit les types de bases classiques: entier (int), floattant (float), caractère (char), chaîne de caractère (string) et booléen (bool). Ces types disposent des opérations usuelles (typées, attention !) et des opérations de comparaison (polymorphes.) Des exemples d'expressions divers seront disséminés dans la suite du cours, pour une référence complète allez voir la doc [12] ou vos cours de sup (idem pour les construction comme if ... then ... else ... .)

Filtrages, motifs et fonctions

OCaml (comme tous les langages de la famille ML) dispose d'un mécannisme de filtrage par motifs (Pattern Matching) très puissant qui combine branchement sur valeur, décomposition et extraction. La décomposition et l'extraction n'ont de sens que sur des valeurs construites (on verra ça plus tard.)

(* exemple de pattern maching *)
let f x = match x with
    0 -> "Zero"
  | 1 | -1 -> "Unité"
  | _ -> "Autre"

On peut combiner le pattern matching et la construction des fonctions annonymes (i.e. construction avec function) pour simplifier certains écritures:

let f = function
    0 -> "Zero"
  | 1 | -1 -> "Unité"
  | _ -> "Autre"

Attention, cette construction ne marche qu'avec function et un paramètre (donc pas avec fun.)

Récursivité

Pour effectuer des opérations répétitives, les langages fonctionnels s'appuient avant tout sur la notion de fonction récursive. En OCaml, pour qu'une fonction puisse être récursive, il faut que son nom existe avant la déclaration de son corps, pour indiquer ce genre de situation, on dispose du mot clef rec qui transforme la déclaration avec let en un point fixe d'une expression récursive. En clair, pour déclarer une fonction récursive, il faut utiliser rec. Voici un petit exemple avec du pattern matching:

(* Factorielle - uniquement avec des entiers positifs ou nul *)
let rec fact = function
    0 | 1 -> 1
  | n -> n * fact (n-1)

Bien qu'il soit possible d'écrire des valeurs récursive avec n'importe quoi, en général, cette construction n'a de sens qu'avec les fonctions.

Types construits

Les types de bases ne sont généralement pas suffisant pour écrire des programmes réels (en théorie, on peut, on peut même tout faire avec comme unique forme de valeurs des fonctions, c'est d'ailleurs le cas pour le modèle théorique derrière ML et les autres langage fonctionnel: le 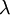$\lambda$ calcul.) OCaml fournit donc la possibilité de construire des valeurs complexes: couples (et n-uplets), enregistrements, injections (types sommes) ...

Les couples sont relativement simples à écrire, ils utilisent la virgule comme séparateur (et en général les parenthèses.) Ils permettent d'associer deux (ou plus) valeurs pour les transmettre de fonctions en fonctions (comme paramètre ou comme résultat.) Ils sont relativement pratiques à utiliser, surtout combiner avec les possibilité du filtrage (et les différents sucres syntaxiques associés.)

(* exemples avec des couples *)
let c1 = (1,2) ;;
let c2 = (1, "foo", 0.3, true) ;;
 
let f x = (x,x * 2) ;;
 
let a = match f 1 with
    (x,_) -> x ;;
let b = match f 1 with
    (_,x) -> x ;;
 
let (a,b) = f 1 ;;
 
let g x = match x with
    (y,z) -> (y+z,y-z) ;;
 
let g (y,z) = (y+z,y-z) ;;
 
let foo = function
    (0,_) -> 0
  | ((1 | -1),_) -> 1
  | (x,y) -> x * y

Les types sommes sont des constructions plus évoluées qui combinent la possibilité d'avoir plusieurs valeurs possibles discrètes (comme avec une énumération) associées chaqu'une à un ensemble de valeurs. On doit pour se faire déclarer un type.

type t =
    Vide
  | Entier of int
  | PairEntier of int * int
  | Chaine of string

On peut ensuite utiliser le filtrage pour connaître la valeur du constructeur (Vide ou Entier ... ) et pour éventuellement tester ou capturer les valeurs associées:

let t2string = function
    Vide -> "Vide"
  | Entier x -> "Entier("^(string_of_int x)^")"
  | PairEntier(x,y) ->
      "PairEntier("^(string_of_int x)^","^(string_of_int y)^")"
  | Chaine s -> s

Les types sommes peuvent être récursifs (on parle de récursion gardée) et donc utilisés pour écrire des structures simplement chaînées, comme des listes ou des arbres:

type int_list =
    Nil
  | Cons of int * int_list ;;
 
let rec long = function
    Nil -> 0
  | Cons (_,l) -> 1 + long l
 
type int_bintree =
    Leaf of int
  | Node of int_bintree * int * int_bintree
 
let rec taille = function
    Leaf _ -> 1
  | Node(fg,_,fd) -> (taille fg) + (taille fd) + 1

OCaml fournit un type de liste polymorphe (qui est en réalité un type somme sur le même principe que le type int_list de l'exemple précédant.) Ce type dispose de deux constructeurs:

• la liste vide: [] (Nil dans notre exemple)
• l'ajout en tête: h::t (Cons(h,t))

(* listes *)
let l1 = [] ;; (* liste vide *)
let l2 = 1::[] ;;
let l3 = 1::2::3::4::5::[] ;;
 
(* sucre (l3 = l4) *)
let l4 = [1;2;3;4;5] ;;
 
(* longueur *)
let rec len = function
    [] -> 0
  | _::t -> 1 + len t;;

Voici quelques exemples avancés (mais très classique) utilisant l'ordre supérieur:

let rec map f = function
    [] -> []
  | h::t -> f h :: map f t
 
let rec forall f = function
    [] -> true
  | h::t -> f h && forall f t
 
let rec fold_left f a = function
    [] -> a
  | h::t -> fold_left f (f a h) t

On peut utiliser les types sommes (combinés avec le polymorphisme) pour renvoyer des valeurs différentes suivant les situations:

type 'a good_or_wrong = Good of 'a | Wrong of string
 
let safe_fact n =
  let rec aux acc = function
      0|1 -> acc
    | x -> aux (acc * x) (x - 1)
  in
    if n < 0 then
      Wrong "Entier négatif"
    else
      Good (aux 1 n) ;;

Un bonne exemple est le type prédéfini 'a option dont la définition est la suivante:

type 'a option = None | Some of 'a

On peut utiliser ce type pour le résultat d'une recherche, comme dans l'exemple suivant, où l'on cherche dans une liste associant des couples de valeur vis à vis du premier membre du couple.

let find x = function
    [] -> None
  | (h,r)::_ when h = x -> Some r
  | _::t -> find x t ;;

La bibliothèque standard

OCaml fournit une bibliothèque de fonctions contenant des opérations pour les types évolués prédéfinis (listes, tableaux ... ), des conteneurs, des opérations d'entrées/sorties évoluées ...

La liste et la description des modules de la bibliothèque standard se trouve dans la doc OCaml (chapitre 20 The standard library[13].) Cette bibliothèque standard est accompagnée d'un module particulier appelé Pervasives contenant toutes les fonctions de bases du langage (chapitre 19 The core library[14].)

Le module Pervasives est toujours ouvert, il n'est donc pas nécessaire d'y faire référence (sauf dans certains cas particuliers.) Par contre, les autres modules de la bibliothèque standard doivent être explicitement ouverts ou référencés pour être utilisés.

Si vous souhaiter ouvrir le module, vous devez utiliser la directive open:

open List
 
let l = [ 1; 2; 3; 4; 5; 6; 7; 8; 9; 10 ]
let i = length l
let main () =
  begin
    print_int i;
    print_newline ();
    exit 0;
  end
let _ = main ()

Mais il est aussi possible d'utiliser la notation pointée pour faire référence au module directement sans avoir à l'ouvrir. Cette méthode est celle que vous devrez presque systématiquement choisir pour éviter les conflits de nom.

let l = [ 1; 2; 3; 4; 5; 6; 7; 8; 9; 10 ]
let i = List.length l
let main () =
  begin
    print_int i;
    print_newline ();
    exit 0;
  end
let _ = main ()

Typage et inférence

Un peu de culture

L'un des éléments important d'OCaml est le typage (en fait l'inférence de type.) Typer un programme consiste à vérifier, sans exécuter le programme, que tous les opérations du programme sont légitime. La notion de typage est fortement liée à la sémantique du langage et pour pouvoir construire un langage fortement typé, il faut que ce langage dispose d'une sémantique formelle bien fondée. En règle général, on décrit (formellement) la sémantique d'un langage sous la forme d'une sémantique opérationnelle dite à petits pas. Cette sémantique décrit en fonction des différentes construcitons du langage l'évolution vers le résultat (la fin de l'exécution) final du programme.

Pour chaqu'une des constructions du langage, il existe au moins une règle qui s'applique si cette construction est bien utilisée, si ce n'est pas le cas, c'est que le terme (le bout de programme en cause) n'est pas bien construit et il n'existe donc pas de résultat pour le programme (en fait, en réalité le programme parts dans un comportement non prévu, s'arrête sur une opération illégale ... )

L'objectif du typage est de détecter ces situations à partir d'une analyse statique du code source. Il existe plusieurs formes de typage: monomorphe, polymorphe, explicite, implicite, avec sous-typage, avec inférence ...

OCaml fait partie des langages polymorphes avec inférence de types (parfois aussi appeller reconstruction de type.) L'idée est que les expressions ne sont pas typées explicitement par le programmeur (sauf cas particulier) et le compilateur va reconstruire le type de chaque expression (et donc vérifier au passage qu'elle est bien formée.) La notion de polymorphisme indique que certaines expressions ou construcitons peuvent admettre plusieurs types, par exemple la fonction suivante:

let id x = x ;;

peut admettre le type int -> int, mais aussi string -> string ou float -> float ! En réalité, cette fonction admet n'importe quel type flêche tel que le domaine soit égal au co-domaine, ce qui plus mathématiquement peut se décrire: quelque soit le type t, la fonction id admet le type t -> t.

Cette forme de type générique est un schéma de type, il exprime la forme la plus générale du type que peut admettre une expression tout en restant bien typée (et donc bien formée.) D'un point de vue théorique, le type id se note: 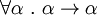$\forall\alpha ~.~ \alpha \rightarrow \alpha$. Le compilateur utilisera la convention suivante: un nom de variable qui commence par un quote est une variable de type et celle-ci est considéré comme quantifiée universellement (dans les schéma de type de ML, la quantificateur est toujours à l'extérieur du type) si le quote n'est pas suivit d'un caractère souligné. Le type de notre fonction id sera donc: 'a -> 'a.

Les variables de types interviennent dans le type des expressions (en général celui des fonctions) mais aussi lorsque l'on déclare des types polymorphes. Par exemple, voici une variante du list avec une valeur en exemple:

type 'a myList = Empty | Cons of 'a * 'a mylist ;;
 
let l = Cons(1,Cons(2,Cons(3,Empty))) ;;

La valeur l a le type: int myList (ce qui indique que la variable de type a été instantiée en type int.)

Principe d'unification

L'algorithme qui reconstruit le type d'une expression est appellé algorithme W, il procède suivant un principe d'unification: à chaque fois qu'il rencontre une contrainte sur une variable de type, il unifie ce qu'il sait sur cette variable avec l'information qu'il vient d'acquérir. Prennons l'exemple suivant:

let f = function g -> function x -> function y -> (g x, g y) ;;

On construit le type de f de la manière suivante:

• on voit que f est une expression de la forme: function g -> e et donc admet comme type: 'a -> 'b où 'a a été choisi pour la variable x et 'b pour le corps de la fonction. Or, e a la forme x -> e', on en déduit 'b = 'c -> 'd. On obtient par le même résultat que 'd = 'e -> 'f. Ce qui nous donne pour l'instant comme type pour f: 'a -> 'c -> 'e -> 'f.

On continue avec l'examun du corps de la fonction, on y voit déjà qu'il s'agit de la construction d'un couple, donc 'f = 'g * 'h. On voit ensuite que le premier membre du couple est le résultat de l'application du paramètre g au paramètre x, on en déduit les contraintes suivantes: 'a = 'i -> 'j, 'c = 'i et 'g = 'j. De même on obtient pour le second membre du couple: 'e = 'i et 'h = 'j. En rassemblant toutes ses informations (en appliquant l'unification) on obtient:

('i -> 'j) -> 'i -> 'i -> 'j * 'j

Ce qui correspond plus ou moins à la réponse d'OCaml (les lettres sont différentes, mais le type est le même.)

Prennons maintenant un exemple plus précis (avec plus de contraintes):

let f g x = (g 1, 1 + g x) ;;

Cette exemple ressemble plus ou moins au précdant, une fonction avec cette fois-ci deux paramètres (g et x) et comme corps un couple où g est utilisé comme une fonction. On peut passer les étapes initiales, on aboutit assez rapidement aux contraintes suivantes:

g : 'a -> 'b (* g est une fonction *)
x : 'c
'a = int     (* g 1 impose que g prenne des int en entrée *)
'c = 'a      (* x est passé en paramètre de g *)
'b = int     (* le résultat de g est utilisé dans une addition *)

La résolution du système d'équation précédante nous donne:

g : int -> int
x : int -> int

Donc on obtient le type de f:

f : (int -> int) -> int -> int * int

Ce qui correspondra bien au typage d'OCaml.

Voyons un dernier exemple avec des listes cette fois-ci:

let rec map f = function
    [] -> []
  | h::t -> f h :: map f t

Il y a deux points particuliers ici: les listes et la récursivité. On va commencer par donner un type à chaque symbole présent dans le corps de map, notamment pour le symbole map lui même (à cause de la récursivité.) On ajoute ensuite les contraintes en fonction des contextes d'utilisation de chaque symbole:

map : 'a
f   : 'b
h   : 'c
t   : 'c list

'a = 'b -> 'd list -> 'f
'f = 'g list
'b = 'c -> 'e
'd = 'c
'g = 'e

map : ('c -> 'e) -> 'c list -> 'e list

Au final, on retrouve le résultat attendu (au nommage de variables de type près.) L'astuve ici est de voir map comme une sorte de paramètre de lui même, dont le type n'est pas encore défini et de l'unifier avec les contraintes d'utilisation rencontrées. En particulier, le type de retour de map correspond au type de chaque branche du filtrage.

Autre point, la valeur [] prend le type générique 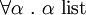$\forall \alpha ~.~ \alpha~\text{list}$ indiquant une liste polymorphe, la variable $\alpha$ sera unifée indépendement en fonction du contexte. De même, le pattern h::t nous impose comme type pour h le type 'a et pour t le type 'a list avec la même variable de type (qui s'unifiera avec la variable de type du pattern [].)

Bien évidement, tout ce travail est automatique, il y a donc un algorithme déterministe derrière tout ça, mais son énnoncé est un peu trop avancé pour ce cours. Ce que vous avez à savoir est relativement simple: tout nouveau symbole implique l'usage d'une variable de type fraiche (qui n'a pas encore été utilisée) qui sera unifiée d'une manière ou d'une autre avec les autres en fonction des situations. Il existe des cas qui nécessite un peu plus de réflexion, mais vous avez une bonne base pour anticiper les problèmes de typage d'OCaml.

Forcer le typage et types non-génériques

Il est parfois nécessaire (en tout cas pratique) de forcer le type d'un paramètres de fonction ou d'une constante définie par un let. Voici quelques exemples:

(* forcer le type de la fonction iter *)
let rec iter (f: 'a -> unit) = function
    [] -> ()
  | h::t -> f h ; iter f t ;;
 
(* forcer le type de contenu d'une liste vide *)
let (l : int list) = [] ;;
 
(* forcer le type de la fonction *)
let f : 'a list -> int list = function
    [] -> []
  | _::t -> t ;;

Dans le dernier exemple, on notera que la réponse d'OCaml est plus précise que le type que nous avons donné (ce qui est logique.)

En terme d'inférence, forcer types n'a rien de bien compliqué: il suffit d'ajouter une contrainte sur les variables de type !

Dans certains cas vous obtenez une variable de type particulière de la forme '_a. Cette variable n'est pas quantifiée: elle est engendrée par l'algorithme d'inférence dans une contexte où elle ne peut pas être généralisée (la raison exacte est liée aux valeurs modifiables, comme les références, que nous verrons au prochain cours) mais où les contraintes d'unification ne permettent pas la déterminer complètement. Prennons un exemple:

let p x y = (x,y) ;;
 
let f = p 1 ;;

Le type de f est '_a -> int * '_a. L'algorithme ne peut généraliser le paramètre implicite de f (puisqu'il n'est pas exprimé.) La variable de type '_a est donc en attente de plus de précision. Notamment, si on applique f à un entier (par exemple), le type de f devient (et ceux pour le reste du programme) int -> int * int.

Construction des programmes OCaml et compilation

Jusqu'à présent vous n'avez fait qu'interpréter vos programme OCaml, mais ce n'est pas le seul usage que vous pouvez faire du langage. OCaml dispose de deux compilateurs sur presques toutes les plateformes: un compilateur natif (ocamlopt) et un compilateur bytecode (ocamlc.)

Le compilateur bytecode produit des binaires pour la machine vituelle ocamlrun (sauf dans certains cas) qui sont donc, presque que cross-plateformes. Le compilateur natif, lui, génère un binaire classique correspondant à l'architecture et au système sur lequel vous êtes. On notera également que les deux compilateurs existe en version bytecode ou native (i.e. ils ont été compilé par ocamlc ou ocamlopt.)

Si en terme d'exécution cela ne fait (presque) pas de différence, les performances ne sont pas les mêmes. Le code produit par le compilateur natif sera en général bien plus rapide que celui produit par le compilateur bytecode. Par contre, la génération du code natif est plus longue. Sur de gros projet, il est parfois intérressant d'effectuer les compilations de tests et de debug en bytecode et de réserver la compilation native pour les tests de performances et la production de l'exécutable final.

Le fait de produire un vrai programme (natif ou bytecode) implique une organisation différente de votre code par rapport à l'interpréteur. En effet, l'interpréteur exécute vos phrases à mesure que vous lui donnez et répond (en mode interractif) en affichant les valeurs correspondantes. Dans un vrai programme, il vous faudra gérer les entrées et les sorties, le déroulement du programme, la ligne de commande de celui-ci ...

Modèle d'exécution

L'exécution d'un programme OCaml suit la logique suivante: chaque phrase rencontrée est exécutée et si elle correspond à une définition le symbole définie est ajouté à l'environnement. Contrairement à la plus part des langages, il n'y a pas de point d'entrée explicite, le début du code (ou du premier module) sert de point d'entrée.

N'importe quelle phrase acceptée par l'interpréteur sera exécutée, mais contrairement au mode interractif de celui-ci, certaines phrases n'auront aucun effet, visible ou réel. Par exemple le programme suivant:

let fact n =
  let rec aux acu = function
      0|1 -> acu
    | x -> aux (acu * x) (x - 1)
  in
    if n < 0 then 0
    else aux 1 n ;;
 
fact 5;;

Une fois compiler, ce programme ne fait ... rien ! En fait, si il calcule un epu, mais il n'affiche rien. Les expressions seules (celles qui sont hors définitions) n'ont en générale aucun effet et je vous conseille (et même vous impose) de ne pas les utiliser. Mais alors, comment fait-on ?

Construction d'un point d'entrée et définition vide

Pour clarifier la situation, on va, artificiellement, construire un point d'entrée. Le principe est simple, vos programme OCaml auront la forme suivante:

• Une série de définitions commencant systématiquement par un let.
• La définition d'une fonction particulière main (ou tout autre nom qui vous plaira) prennant un paramètre de type unit.
• Le point d'appel de la fonction principalle grace à la construction let _ = ...

Bien évidement, il va nous falloir lire et écrire sur la sortie et l'entrée standard et même récupérer les paramètres de la ligne de commande. Reprennons notre exemple et ajoutons notre point d'entrée:

(* fact.ml *)
 
(* definitions *)
let fact n =
  let rec aux acu = function
      0|1 -> acu
    | x -> aux (acu * x) (x - 1)
  in
    if n < 0 then 0
    else aux 1 n
 
(* fonction principale *)
let main () =
  begin
    print_int (fact 5);
    print_newline ();
    exit 0;
  end
 
(* point d'entrée *)
let _ = main ()

On peut maintenant compiler et exécuter ce programme:

> ocamlc.opt -o fact fact.ml
> ./fact
120

On peut également voir la différence entre les deux types de compilations:

> ocamlc.opt -o fact.byte fact.ml
> ocamlopt.opt -o fact.opt fact.ml
> file fact.byte fact.opt
fact.byte: a /usr/local/bin/ocamlrun script text executable
fact.opt: ELF 32-bit LSB executable, Intel 80386, version 1 (FreeBSD),
for FreeBSD 7.2, dynamically linked (uses shared libs), FreeBSD-style,
not stripped

Utilisation des compilateurs

Les deux compilateurs OCaml s'utilisent presque de la même manière. Dans un permier temps (tant que l'on ne fera pas de module) leur ligne de commande seront même identiques. Décomposons l'exemple précédant:

> ocamlc.opt -o fact fact.ml

Le compilateur utilisé est le compilateur bytecode (mais dans sa version native, essayez file `which ocamlc` `which ocamlc.opt` pour voir la différence) il y a deux paramètres:

• -o fact : le flag -o permet de donner le nom du fichier à produire, ici fact. Si ce paramètre est absent, le compilateur produit le fichier a.out
• fact.ml : le nom du fichier source

L'ordre importe peu ici, du moment que le flag -o est TOUJOURS suivi du nom du fichier de destination (ici fact.)

Le nom du compilateur peut être remplacé par ocamlc (le même, mais compilé en bytecode), ocamlopt.opt ou ocamlopt. Pour l'instant, la seule différence notable (hors performance) sera les autres fichiers produits. En effet, le compilateur engendre des fichiers objets qui servent pour l'édition de liens. Voici la liste des fichiers produits en fonction du compilateur:

Commande	Fichiers produits
ocamlc -o cible fichier.ml ou ocamlc.opt -o cible fichier.ml	cible fichier.cmo fichier.cmi
ocamlopt -o cible fichier.ml ou ocamlopt.opt -o cible fichier.ml	cible fichier.cmx fichier.cmi fichier.o

Typage seulement

Il est possible de demander au compilateur de ne réaliser que la phase de typage de votre fichier. La sortie obtenue pourra être utilisée par la suite comme interface de module. Pour l'instant, l'intérêt pour nous est de vérifier nos programme et de comprendre les résultat du typage. Pour activer cette possibilité, il faut ajouter le flag -i.

$ ocamlc -i fact.ml
val fact : int -> int
val main : unit -> 'a

On retrouve bien le type de notre fonction factorielle (int -> int) et le type de notre fonction main (on notera au passage que cette fonction quitte via la fonction exit dont le type de retour n'est pas déterminer puisqu'elle ne revient jamais et que par conséquent notre fonction main n'a pas non plus de type de retour vraiment défini.)

Conclusion

Nous avons fait le point sur les bases essentielles du langage OCaml. Nous avons également vu comment écrire un vrai programme OCaml, bien que pour l'instant, il nous manque encore quelques éléments comme l'accès à la ligne de commande, la gestion des entrées utilisateur et surtout les modules et la compilation séparée.

Cours	Partie
Cours de Programmation EPITA/spé	Programmation:OCaml