MiniProj:C:2014

I Want Out !

Doctor Stein grows funny creatures and let them run into the night ! ...

Le docteur Stein élève des droles de créatures dont l'objectif est d'explorer des donjons. Il a décidé de se limiter aux donjons de la guilde des explorateurs amateurs pour lesquels une carte est fournie. Mais la carte n'est pas toujours suffisante, il faut que le docteur fournisse un chemin à suivre à ses créatures !

Votre objectif est de fournir au Docteur Stein un chemin sûr (c'est à dire un chemin où il ne perd pas la vie) dans le donjon entre deux salles particulières du donjon. L'idéal étant que ce chemin soit le plus court.

Présentation des donjons

Les donjons de la guilde des explorateurs amateurs ont une forme commune: il dispose de certains types de salles (voir plus loin) reliées entre elles par des couloirs. La traversée d'un couloir est plus ou moins difficile et la difficulté est indiquée sur la carte. La difficulté d'un couloir peut dépendre du sens de parcours, il est même possible que certains couloirs ne puissent être franchis que dans un sens. Chaque salle porte un numéro unique dans le donjon qui permet de les identifier facilement. Les différents types de salles sont les suivants:

• Salle ordinaire
• Tannière de monstre: un monstre se cache dans ces salles, la carte indique le coût du combat contre le monstre.
• Piège mortelle: ces salles sont des culs-de-sac dont il est impossible de repartir (entrainnant la mort de l'explorateur s'il a le malheur de s'y rendre.)
• Gargotte: les gargottes des donjons sont tenues par les gnomes de la guilde et permettent aux explorateurs de retrouver des forces pendant leur exploration. Chaque gargotte propose un menu unique (toujours disponible) dont l'effet revigorant est indiqué sur la carte.

Le niveau de vie de l'explorateur

Chaque explorateur de donjons dispose d'un certain niveau de vie au début de sa quête. L'unité de mesure des niveaux de vie a été unifiée avec les niveaux de difficultés des couloirs, le niveau des monstres et l'apport des repas des gargottes. Par conséquent, il est très simple de calculer le coût d'un chemin d'une salle à une autre dans le donjon et de le comparer au niveau de vie de l'explorateur.

L'explorateur meurt lorsque son niveau de vie tombe à 0 (ou en dessous) dans la salle d'arrivée. Notamment, lorsque l'explorateur arrive dans une gargotte, il ne meurt que si son niveau de vie n'est plus positif après avoir manger.

Le mini-projet

Comme vous l'aurez compris il s'agit ici de trouver des chemins dans un graphe. Le projet se découpe en plusieures phases:

1. Lecture du graphe à partir d'un fichier et validation de chemin (4 points);
2. Recherche de chemin simple dans le graphe (5 points);
3. Résistance et montée en charge (9 points).

En outre, deux points seront accordés au respect des règles de rendu (rendu dans les temps et au format attendu.)

Format du fichier de description du donjon

Le format de description est un format texte relativement simple:

• Les salles sont numérotées de manière continue à partir de 1
• Les coûts sont des entiers sur 64bits signés (même si dans les fichiers, ils seront toujours exprimés positivement.)
• Les lignes commençant par le caractère "#" sont des commentaires et doivent être ignorées
• Les lignes vides doivent être ignorées
• La première ligne ayant du sens (ni vide, ni commentaire) doit avoir la forme "ROOMS: n" où n est un entier strictement positif représentant le nombre de salles du donjon.
• Les lignes suivantes indiquent quels types de salles sont disponibles. Elles ont la forme suivante:
  • "MONSTER: s c" indique que la salle s contient un monstre de niveau c.
  • "DEAD: s" indique que la salle s est un piège mortelle.
  • "BREWERY: s c" indique que la salle s est une gargotte qui sert un menu de niveau c
  • Les salles qui n'apparaissent pas dans l'une des catégories sont des salles ordinaires.
• Une fois que toutes les salles sont décrites, on peut lister les couloirs. La partie couloirs est introduites par la ligne "TUNNELS"
• Chaque couloir est décrit par une ligne de la forme: "TUNNEL: s1 c s2" indiquant l'existance d'un couloir de la salle s1 jusqu'à s2 avec pour coût c.

Un donjon

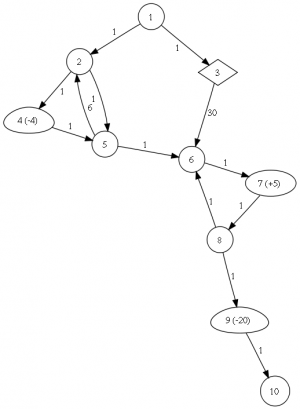
Voici un exemple de description de donjon:

# Salles
ROOMS: 10
MONSTER: 4 4
MONSTER: 9 20
BREWERY: 7 5
DEAD: 3

# couloirs
TUNNELS
TUNNEL: 1 1 2
TUNNEL: 1 1 3
TUNNEL: 2 1 4
TUNNEL: 2 1 5
TUNNEL: 3 30 6
TUNNEL: 4 1 5
TUNNEL: 5 6 2
TUNNEL: 5 1 6
TUNNEL: 6 1 7
TUNNEL: 7 1 8
TUNNEL: 8 1 6
TUNNEL: 8 1 9
TUNNEL: 9 1 10

Remarque: la guilde garantie des cartes bien formées, vous n'aurez donc pas à gérer les erreurs de parsing.

Format des chemins

Les chemins seront représenté par le format suivant: [s1;...;sn] (sans espace) où les si sont les numéros des salles traversées par le chemin dans l'ordre (bien sûr.) On notera au passage que le format des chemins correspond à l'affichage d'une liste, votre programme devra donc supporté la présence éventuelle d'un point-virgule suplémentaire à la fin, par exemple les chaînes suivantes sont toutes les deux des chemins valides (elles représentent le même chemin):

[1;2;3]
[1;2;3;]

Affichage du coût d'un chemin

Lorsque l'utilisateur rentre la commande COST v [s1;..;sn], vous devez calculer le coût (et la longueur, en sommet) du chemin avec v points de vie au départ. L'affichage se fera de la manière suivante:

• (c,l) si le nombre de points de vie était suffisant, c est le nombre points de vie restant à la fin du chemin et l est la longueur du chemin (nombre de sommets.)
• DEAD si le nombre de point de vie n'était pas suffisant, où si le chemin contient un piège mortel.
• NP si le chemin n'est pas valide (salle inexistante, pas de couloir permettant le parcours ... )

Voici un exemple de session sur le graphe décrit plus haut:

COST 10 [1;2;4;]
(4,3)
COST 1 [1;2;4;]
DEAD
COST 2 [1;4]
NP

Recherche de chemin

La commande PATH v s e demande à votre programme de chercher un chemin entre la salle s et la salle e avec v point de vie au départ. Votre programme devra alors soit afficher le chemin, soit afficher NP s'il n'existe pas de chemin possible (pas de couloir, pas assez de point de vie ... )

Votre programme

Votre programme devra s'appeler stein et prendra en paramètre le nom du fichier de description du donjon. Une fois le donjon lu, il devra attendre une commande sur son entrée standard:

• COST v [s1;...;sn] lui demandera de calculer le coût du chemin.
• PATH v s e lui demandera la recherche d'un plus court chemin.

Après l'exécution de la commande, votre programme affiche le résultat (en fonction de la commande) et attend une nouvelle entrée. Le programme devra quitter à la réception du caractère de fin de fichier (que l'on peut envoyer depuis le shell en faisant ^D.)

Comme d'habitude, vous devez respecter les formats d'affichage pour que la moulinette reconnaisse votre résultat (attention aux espaces et aux majuscules/minuscules.)

Exemple de session de tests

On considère le graphe décrit précédemment sauvé dans le fichier graphe.dj. On regroupera les tests dans le fichier test-graphe dont le contenu est le suivant:

COST 10 [1;2;5;6;7;8;9;10]
COST 10 [1;2;5;6;7;8;6;7;8;6;7;8;6;7;8;6;7;8;6;7;8;6;7;8;6;7;8;9;10]
COST 10 [1;3;6;7;8;9;10]
COST 10 [1;2;6;8;9;10]
PATH 10 1 4

Enfin, le test du programme donnera les résultats suivants:

> ./stein graphe.dj < test-graphe
DEAD
(2,29)
DEAD
NP
[1;2;4]
>

Votre rendu

Vous rendrez une archive sous la forme: login-donjon2014.tar.bz2 cette archive doit se décompresser dans un répertoire dont le nom est login-donjon2014 contenant:

• Un fichier AUTHORS au format habituel.
• Un makefile qui accepte les cibles all, stein et clean
• Votre code source.

Pour information la moulinette procedera comme suit:

tar xf login-donjon2014.tar.bz2
cd login-donjon2014
make clean
make

Puis effectuera les tests sur le binaire stein.

Note: format du fichier AUTHORS
Ce fichier contient une ligne (vous êtes seul sur le projet) commençant par une étoile (*) suivie d'un espace puis de votre login, le reste de la ligne est ignoré. Attention, votre fichier ne devra contenir qu'une seule ligne et celle-ci devra être correctement terminée (saut de ligne.) Par exemple:

> whoami
foo_b
> cat AUTHORS
* foo_b (Foo Bar)
> cat -e AUTHORS
* foo_b (Foo Bar)$
>

Dates

Le rendu du projet est prévu pour le Vendredi 18 avril 2014 à 23h42. L'interface de rendu sera ouverte à partir du dimanche 13 avril 19h42. Un lien vers celle-ci sera fournie le jour même ici et sur la page d’accueil.

Le rendu se fait ici : [1]

Évalution

La moulinette effectue les évaluations en cascade. Chaque phase est testée avec un certain nombre de cas et le taux de réussite donne la note de la phase.

On rappelle que les évaluations sont automatiques et sont basées sur les sorties décrites dans le présent sujet. Si vous ne respectez pas les formats attendus, vous n'aurez pas les points. Faîtes donc bien attention à vos affichages, aucune réclamation ne sera acceptée.

Niveau 0: rendu

(2 points)

Cette phase est le point de passage obligatoire. Elle n'est pas validée si (pas de points):

• le fichier AUTHORS manque ou est mal formé

De plus, les autres niveaux ne sont pas évalués si:

• l'archive n'est pas au format tar+bzip2
• l'archive ne se décompresse pas du tout;
• l'archive ne se décompresse pas dans la bon répertoire;
• il n'y a pas de Makefile;
• l'une des règles attendue dans le Makefile ne marche pas;
• le binaire produit ne porte pas le bon nom.

En particulier, vous devez vous assurez que la séquence d'action suivante se déroule sans erreur:

tar xjf login-donjon2014.tar.bz2 login-donjon2014
cd login-donjon2014
make clean
make

Si aucune erreur n'arrête cette séquence et que le répertoire courant contient bien un binaire exécutable appelé stein, alors la moulinette passe aux étapes suivantes.

Note: la commande make clean ne doit pas échouer, même si les fichiers qu'elle tente d'effacer n'existent pas. Pour s'assurer que tout va bien, essayer de faire make clean && make clean, s'il n'y a pas de message d'erreur, tout va bien. Sinon, en géneral, man 1 rm est une bonne piste …

Niveau 1: validation/évaluation de chemin

(4 points)

Cette phase sert principalement à vérifier que vous êtes capable de charger un graphe. Elle est évaluée par deux séries de tests simples:

• Test avec une commande par session
• Tests avec plusieurs commandes par session

Dans tous les cas, la seule commande utilisée sera COST.

Niveau 2 et 3: recherche de chemin et montée en charge

Les deux derniers niveaux sont testés suivants le même schéma global. Pour chaque test, un graphe est chargé puis on demande un chemin dans ce graphe. Le résultat de chaque test est calculé comme suit:

• 0 points si votre programme ne répond pas (erreur d'exécution, timeout ... ) ou si le chemin renvoyé n'est pas valide.
• 1 point si votre programme renvoie un chemin valide.
• 3 points si votre programme renvoie un chemin valide et que ce chemin est minimal (la longueur du chemin correspond au nombre de salle du chemin.)

Enfin, une fois tous les tests passés, le nombre de points accumulés est ramené sur le nombre de points de la tranche.

À quelques détails prets, la différence entre chaque phase de tests correspond à la difficulté des cas testés.

Les chemins recherchés existeront toujours.

Niveau 2: Chemins simples

(5 points)

Dans ce niveau, les chemins cherchés sont sans circuits absorbants, ce sont des chemins élémentaires (relativement court.)

Niveau 3: montée en charge

Ce niveau est découpé en trois parties:

Support des circuits absorbants

(3 points)

Comme l'explorateur peut regagner des points de vie, il est possible de boucler autour des gargottes (en utilisant les circuits du graphe) pour accumuler suffisament de points de vie pour passer un arc avec un fort coût ou un monstre. Tous les chemins cherchés dans cette partie nécessite au moins une boucle dans un circuit.

Pour la gestion des circuits absorbants. je vous recommande la lecture des conseils un peu plus loin !

Longs chemins

(3 points)

Cette partie est la prolongation de la précédante, les chemins recherchés contiendront forcément des circuits, mais de plus ces chemins seront longs, au moins plusieurs centaines, voir plusieurs milliers de salles.

Les tests sur cette partie pouvant être relativement long, ceux-ci ne seront fait sur votre projet que si votre programme trouve un chemin valide pour au moins 60% des tests de la partie précédantes.

Sessions longues

(3 points)

Cette partie va tester l'endurance de votre programme: chaque session (chaque exécution) comportera plusieurs recherches de chemin (avec ou sans circuits.) Les chemins ne seront pas forcément longs, l'objectif est de vérifier que vous gérer bien votre mémoire.

Conseils

Cette partie présente quelques conseils d'implémentation (graphes, algorithmes ... ) mais ce ne sont que des conseils que vous êtes libre de suivre ou pas.

Stratégie de réalisation du projet

Commencons par vous rappeller quelques commandements de la programmation:

Make it right before you make it fast. Make it clear before you make it faster. Keep it right when you make it faster.
- P. J. Plauger - Kernighan and Plauger, The Elements of Programming Style by Brian W. Kernighan, P. J. Plauger , ISBN:0070342075

We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%.A good programmer will not be lulled into complacency by such reasoning, he will be wise to look carefully at the critical code; but only after that code has been identified
- Donald Knuth: Structured Programming with Goto Statements[2]. Computing Surveys 6:4 (1974), 261–301

The First Rule of Program Optimization: Don't do it. The Second Rule of Program Optimization (for experts only!): Don't do it yet.
- Michael A. Jackson[3].

More computing sins are committed in the name of efficiency (without necessarily achieving it) than for any other single reason - including blind stupidity.
- W.A. Wulf[4]

Votre objectif premier est de faire marcher votre projet. L'optimisation devra venir après. Maintenant, il y a des stratégies plus efficace pour pouvoir optimiser facilement votre code.

Les conseils sont toujours les mêmes:

• Modéliser correctement votre projet avant de commencer à coder.
• Garder une approche abstraite, toutes vos structures de données doivent être accédées uniquement au travers d'opérations abstraites (encapsulation.)
• Privilégier l'algorithme principal: les structures annexes (comme les ensembles d'ouverts et de fermés) seront des points d'optimisation ultérieurs.
• Implémenter les structures secondaires en privilégiant la correction avant la performance, ça vous permettra de tester votre algos, une fois l'algo validé vous pourrez changer d'implémentation pour vos structures.
• Ne négliger pas la gestion de la mémoire, mais là encore, garder une approche abstraite pour pouvoir changer d'allocateur lors de la phase d'optimisation.
• Le premier pallier est là pour vous aider: vous aurez besoin de vérifier vos chemins, utiliser la commande demandée (COST) pour vérifier vos chemins et obtenir leur taille.

Représentation des graphes

Les extraits de codes qui suivent sont donnés à titre indicatif et ne fonctionnent pas forcément (ils ne sont pas complets ni cohérents.)

Il existe plusieurs façon de représenter les graphes, notamment les versions vues en TD d'algo. Je vous propose ici une version plus compacte et plus pratique basée sur la version full-dynamique du TD mais utilisant des tableaux pour la liste de sommet.

typedef struct s_graph *t_graph;
typedef struct s_som   *t_som;
typedef struct s_adj   *t_adj;
 
struct s_som
{
  int	som;
  t_adj	succ, pred;
};
 
struct s_adj
{
  float	cost;
  int	vsom;
  t_adj	next;
};
 
struct s_graph
{
  int		order;
  t_som		lsom[1];
};

Le graphe est composé d'un tableau de pointeur de sommet (dont la taille est donné par le champ order) et chaque sommet contient deux listes d'adjacence (listes d'arcs) pour les successeurs et les prédecesseurs. Les éléments des listes d'adjacence indique le coût (avec un float) et le numéro du sommet (sa case dans le tableau.)

Voici quelques fonctions/macros utiles:

#define GSIZE(o) (sizeof(int) + sizeof(t_som)*(o))
#define room(g,s) (g->lsom[(s)])
#define succ(g,s) (room(g,s)->succ)
#define pred(g,s) (room(g,s)->pred)
#define next(p) ((p)=(p)->next)
 
t_graph create_graph(int order)
{
  t_graph	g;
  int		i;
  g = malloc(GSIZE(order));
  g->order = order;
  for (i=0; i<order; i++)
    {
      room(g,i) = malloc(sizeof(struct s_som));
      room(g,i)->som = i;
      succ(g,i) = pred(g,i) = NULL;
    }
  return g;
}
 
void add_arc(t_graph g, int s, int d, float c)
{
  t_adj		pa;
  pa = malloc(sizeof(struct s_adj));
  pa->cost = c;
  pa->vsom = d;
  pa->next = succ(g,s);
  succ(g,s) = pa;
  pa = malloc(sizeof(struct s_adj));
  pa->cost = c;
  pa->vsom = s;
  pa->next = pred(g,d);
  pred(g,d) = pa;
}

Plus courts chemins

Il existe de nombreux algorithme de plus court chemin, mais si vous observez bien notre problème, ces algorithmes ne s'applique pas bien. En effet, Dijkstra et ses variantes ne marchent pas avec des coûts négatifs, or les salles permettant de gagner des points de vie impliquent l'existence de coûts négatifs. L'algorithme de Bellman basé sur le demi-degré intérieur supporte les coûts négatifs mais pas les cycles, or dans certains donjons il peut être nécessaire d'utiliser les circuits absorbants pour arriver à la sortie, ce qui exclut non-seulement Bellman mais aussi Bellman-Ford.

Comment faire ?

La solution est plus simple qu'il n'y parait. En réalité, ce n'est pas un problème d'algorithme, mais un problème de données. En effet, le plus court chemin qui nous intéresse ne dépend pas réellement du coût du chemin (sauf pour rester en vie) mais du nombre de salles traversées.

La solution consiste à effectuer la recherche dans un graphe dérivé de l'original que l'on appelle graphe d'états. Le principe est simple, chaque sommet (ou état) du graphe représente une salle du donjon et le nombre de point de vie de l'explorateur lorsqu'il a visité cette salle. Les arcs décrivent le passage d'une salle à une autre (avec la modification de point de vie correspondante) et ont un coût unique de 1.

Ce graphe représente donc l'ensemble des situations possibles où l'explorateur reste en vie. Il est bien évidement beaucoup plus grand que le donjon. L'avantage de cette méthode est que la recherche du plus court chemin ne fait plus intervenir de coût, on peut donc utiliser Dijkstra ou une de ses variantes (comme A*), voir un simple parcours largeur.

Le graphe d'état étant relativement important (possiblement infini) et dépendant du nombre de points de vie de l'explorateur, on ne cherchera pas à le représenter concrètement, on utilisera plutôt une fonction de transition qui à partir d'une salle et d'un nombre de point de vie fournira un ensemble de couple (salle,point de vie) à partir du graphe du donjon.

Ce graphe peut avoir des circuits: il est tout à fait possible qu'un chemin dans le graphe du donjon nous ramène à une salle déjà visitée avec le même nombre de point de vie. Il est forcément orienté (chaque arc marque la traversée d'un couloir et le gain ou la perte de points de vie correspondant, la traversée dans l'autre sens n'inverse pas ce gain ou cette perte.)

Exemple

Soit le donjon suivant:

ROOMS: 6
MONSTER: 5 13
BREWERY: 3 6

TUNNELS
TUNNEL: 1 1 2
TUNNEL: 2 1 3
TUNNEL: 3 1 4
TUNNEL: 4 1 2
TUNNEL: 4 1 5
TUNNEL: 5 1 6

On veut aller de la salle 1 à la salle 6 avec 10 points de vie. Il va nous falloir passer plusieur fois par la taverne de la salle 3 avant d'avoir suffisamment de points de vie pour passer le monstre de la salle 5. Plus exactement le chemin sera: [1;2;3;4;2;3;4;5;6] ce qui correspond aux états: (1,10), (2,9), (3,14), (4,13), (2,12), (3,17), (4,16), (5,2), (6,1).

Algorithmes exploitables

Parcours largeur

donne les plus courts chemins (mais tests beaucoup trop de sommets);

Bellman

non applicable (présence de cycle);

Dijkstra

donne les plus courts chemins et en testant moins de sommets qu'un parcours largeur;

A*

au moins aussi bon que Dijkstra, mais il faut faire attention aux heuristiques choisies, toutes ne permettent pas de trouver le plus court chemin;

Bellman-Ford

il n'y a pas de circuit absorbant (pas de coût négatif) donc il est applicable mais reste plus couteux que Dijkstra;

Les autres ...

il existe beaucoup d'autre algorithme de recherche de chemins, notamment, il existe peut être des algorithmes pouvant répondre sur le graphe du donjon ... à vous de voir et de chercher.

Attention, il existe des optimisations (même sur le parcours largeur) intelligentes sur ces algorithmes.

Le tournoi de la guilde des donjons

Le but du tournoi est de comparer les performances de vos projets. Bien évidement, seuls les projets dépassant un certain seuil seront inscrit au tournoi.

Pour chaque donjon du tournoi vous obtenez une note contenant deux indicateur: un mallus et votre temps d'exécution. Le mallus est calculé suivant la formule suivante:

• 0: si le chemin est valide et minimal
• 1: si le chemin est valide mais non minimal
• 4: si votre programme atteint le time-out (dans ce cas le temps obtenu ne sera pas utilisé.)
• 7: votre programme renvoie un chemin non valide.
• 8: votre programme s'arrête sur une erreur.

La note finale pour le classement est un triplet composé de la somme des mallus, le nombre de chemins valides renvoyés et de la moyenne des temps d'exécution. Le classement final est un tri lexicographique sur le triplet (mallus, nombre de chemins valides, temps moyen). Par conséquent, les projets qui ne répondent pas toujours correctement seront forcément moins bien classé que ceux qui répondent correctement à chaque fois.

(attention, les règles de classements pourraient changer d'ici le tournoi.)

Pour exemple, voici un donjon qui pourrait être utilisé pour le tournoi:

# Salles
ROOMS: 22
MONSTER: 4 4
MONSTER: 9 80000
MONSTER: 12 12
MONSTER: 14 30
MONSTER: 17 10
MONSTER: 22 80000
BREWERY: 16 1
BREWERY: 18 10
BREWERY: 7 6
BREWERY: 11 17
DEAD: 3

# couloirs
TUNNELS
TUNNEL: 1 1 2
TUNNEL: 1 1 3
TUNNEL: 2 1 4
TUNNEL: 2 1 5
TUNNEL: 3 30 6
TUNNEL: 4 1 5
TUNNEL: 5 6 2
TUNNEL: 5 1 6
TUNNEL: 6 1 7
TUNNEL: 7 1 8
TUNNEL: 8 1 5
TUNNEL: 8 1 13
TUNNEL: 8 10 9
TUNNEL: 6 2 18
TUNNEL: 9 1 20
TUNNEL: 9 1000 10

TUNNEL: 5 1 11
TUNNEL: 11 1 12
TUNNEL: 12 1 13
TUNNEL: 13 1 5
TUNNEL: 13 1 14
TUNNEL: 14 1 15
TUNNEL: 15 1 16
TUNNEL: 16 1 17
TUNNEL: 17 1 15
TUNNEL: 17 1 18
TUNNEL: 18 1 15
TUNNEL: 17 1 19
TUNNEL: 19 1 9

TUNNEL: 20 1 19
TUNNEL: 20 1 18
TUNNEL: 18 20 20
TUNNEL: 20 1 21
TUNNEL: 21 1 22
TUNNEL: 22 1000 10

Avec le chemin de 1 à 10 et 10 points de vie au départ. Pour information, le plus court chemin (ou les plus courts chemins) font exactement 162008 sommets.

Ce donjon (variation du précédant) est aussi assez intérressant. Le chemin est plus court (27667 sommets de 1 à 10 avec 3 points de vie), mais les possibilités de boucle sont plus complexes (la différence entre un Dijkstra classique et un A* modifié devient vraiment flagrante.)

# Salles
ROOMS: 22
MONSTER: 4 4
MONSTER: 9 400000
MONSTER: 12 12
MONSTER: 14 30
MONSTER: 17 10
MONSTER: 22 400000
BREWERY: 16 1
BREWERY: 18 50
BREWERY: 7 6
BREWERY: 11 17
DEAD: 3

# couloirs
TUNNELS
TUNNEL: 1 1 2
TUNNEL: 1 1 3
TUNNEL: 2 1 4
TUNNEL: 2 1 5
TUNNEL: 3 30 6
TUNNEL: 4 1 5
TUNNEL: 5 6 2
TUNNEL: 5 1 6
TUNNEL: 6 1 7
TUNNEL: 7 1 8
TUNNEL: 8 1 5
TUNNEL: 8 1 13
TUNNEL: 8 10 9
TUNNEL: 6 2 18
TUNNEL: 9 1 20
TUNNEL: 9 1000 10

TUNNEL: 5 1 11
TUNNEL: 11 1 12
TUNNEL: 12 1 13
TUNNEL: 13 1 5
TUNNEL: 13 1 14
TUNNEL: 14 1 15
TUNNEL: 15 1 16
TUNNEL: 16 1 17
TUNNEL: 17 1 15
TUNNEL: 17 1 18
TUNNEL: 18 1 15
TUNNEL: 17 1 19
TUNNEL: 19 1 9

TUNNEL: 20 1 19
TUNNEL: 20 1 18
TUNNEL: 18 20 20
TUNNEL: 20 1 21
TUNNEL: 21 1 22
TUNNEL: 22 1000 10