20160926:Practical:C:HomeWork

Sommaire

1 Introduction
- 1.1 Code submission instructions
2 Archive format
3 Provided Files
4 Task: math_func.c
5 Testing with provided code

Introduction

This homework serves as a quick introduction to C and Linux in our environment. It is due on Monday, october 3, 2016 at 2pm.

Code submission instructions

You must build your tarball (see next section) respecting all the instructions and put the file (named: login-20160926-homework.tar.bz2 with login replaced by your login) at the root of your AFS shared directory.

shell> cp login-20160926-homework.tar.bz2 ~/afs/

Archive format

You must build a compressed archive using tar(1) in the format tar.bz2. This archive must contain a directory, named after your login respecting the following structure:

login
- AUTHORS
- Makefile (provided file)
- main.c (provided file)
- math_func.h (provided file)
- math_func.c (your work)

The AUTHORS file will contains your login preceded by a star (*) like this:

* login

It's important that this file contains one single newline character, you can check it using the -e option of cat, this way:

shell> cat AUTHORS 
* login
shell> cat -e AUTHORS
* login$
shell>

In order to build the archive, you must be outside of the directory and invoke the command this may (see the man page of tar(1) for more details):

shell> ls
login
shell> tar cjf login-20160926-homework.tar.bz2 login

You can check the content of your archive by:

moving to another location and unarchiving it
list the content of the archive

Here is some manipulation examples:

shell> ls login/
AUTHORS  Makefile  main.c  math_func.c	math_func.h
shell> tar cjvf login-20160926-homework.tar.bz2 login/
login/
login/math_func.c
login/AUTHORS
login/math_func.h
login/main.c
login/Makefile
shell> file -z login-20160926-homework.tar.bz2 
login-20160926-homework.tar.bz2: POSIX tar archive (GNU) (bzip2 compressed data, block size = 900k)
shell> tar tf login-20160926-homework.tar.bz2 
login/
login/math_func.c
login/AUTHORS
login/math_func.h
login/main.c
login/Makefile
shell> cp login-20160926-homework.tar.bz2 /tmp/
shell> cd /tmp/
shell> tar xf login-20160926-homework.tar.bz2 
shell> cd login
shell> ls
AUTHORS  Makefile  main.c  math_func.c	math_func.h
shell>

Provided Files

These files provide element for testing your code.

`Makefile`

# EPITA Practical Programming S3 - 2016/2017
# Makefile
# Marwan Burelle
 
# Compilers and options
CC=gcc
CPPFLAGS= -MMD
CFLAGS= -Wall -Wextra -std=c99 -pedantic -O2
LDFLAGS=
LDLIBS=
 
SRC = math_func.c main.c
OBJ = ${SRC:.c=.o}
DEP = ${SRC:.c=.d}
 
all: main
 
main: ${OBJ}
 
-include ${DEP}
 
clean:
	rm -f ${OBJ} ${DEP}
	rm -f main
 
# END

All files in this directory must have the proper encoding (ASCII for Unix with single newline character).

`main.c`

# include <err.h>
# include <stdlib.h>
# include <stdio.h>
 
# include "math_func.h"
 
typedef unsigned long (*functype)(unsigned long);
 
const functype ops[] = {
  fact,
  fibo,
  int_sqrt,
  digit_number,
  binary_digit_number,
  power_of_2,
  divisor_sum
};
 
const char *op_names[] = {
  "fact",
  "fibo",
  "int_sqrt",
  "digit_number",
  "binary_digit_number",
  "power_of_2",
  "divisor_sum"
};
 
const char usage[] =
  " <op> <min> <max>\n"
  "\tOperators:\n"
  "\t\t0: factorial\n"
  "\t\t1: fibonacci\n"
  "\t\t2: integer square root\n"
  "\t\t3: number of digits\n"
  "\t\t4: number of binary digits\n"
  "\t\t5: power of 2\n"
  "\t\t6: sum of divisors\n";
 
static
void test(size_t op, unsigned long minval, unsigned long maxval) {
  for (size_t i = minval; i <= maxval; ++i) {
    printf("%s(%lu) = %lu\n", op_names[op], i, ops[op](i));
  }
}
 
int main(int argc, char *argv[]) {
  if (argc < 4)
    errx(1, "%s", usage);
  unsigned long op, minval, maxval;
  op = strtoul(argv[1], NULL, 10);
  minval = strtoul(argv[2], NULL, 10);
  maxval = strtoul(argv[3], NULL, 10);
  test(op, minval, maxval);
  return 0;
}

`math_func.h`

/* math_func.c: some  maths fuctions */
 
# ifndef EPITA_IP_S3_20160926_HOMEWORK_MATH_FUNC_H_
# define EPITA_IP_S3_20160926_HOMEWORK_MATH_FUNC_H_
 
/* fact(n) computes factorial of n              */
unsigned long fact(unsigned long n);
 
/* fibo(n) computes fibonacci number of rank n  *
 * fibo(0) is defined as 0                      *
 * fibo(1) is defined as 1                      *
 * fibo(n) is defined as fibo(n-1) + fibo(n-2)  */
unsigned long fibo(unsigned long n);
 
/* int_sqrt(n) returns the integer part of the  *
 * square root of n using the heron method      */
unsigned long int_sqrt(unsigned long n);
 
/* digit_number(n) compute the number of digits *
 * of n in base-10                              */
unsigned long digit_number(unsigned long n);
 
/* binary_digit_number(n) compute the required  *
 * number of bits of n in base 2                */
unsigned long binary_digit_number(unsigned long n);
 
/* power_of_2(n) returns 2 to power the power n */
unsigned long power_of_2(unsigned long n);
 
/* divisor_sum(n) returns the sum of all the    *
 *  divisors of n including 1 but not n         */
unsigned long divisor_sum(unsigned long n);
 
# endif

Task: `math_func.c`

Your job is to implement the function listed in math_func.h.

Here is a template for the file math_func.c (containing only functions' prototypes.)

/* Home Work */
 
# include <stdlib.h>
 
# include "math_func.h"
 
unsigned long fact(unsigned long n) {
  // FIX ME
}
 
unsigned long fibo(unsigned long n) {
  // FIX ME
}
 
unsigned long int_sqrt(unsigned long n) {
  // FIX ME
}
 
unsigned long digit_number(unsigned long n) {
  // FIX ME
}
 
unsigned long binary_digit_number(unsigned long n) {
  // FIX ME
}
 
unsigned long power_of_2(unsigned long n) {
  // FIX ME
}
 
unsigned long divisor_sum(unsigned long n) {
  // FIX ME
}

The header file math_func.h contains comments giving quick descriptions for each functions, more details follows.

`fact(n)`

The classical factorial function for unsigned long integers (64bits wide in our env).

Running using provided tests:

shell> ./main 0 0 19
fact(0) = 1
fact(1) = 1
fact(2) = 2
fact(3) = 6
fact(4) = 24
fact(5) = 120
fact(6) = 720
fact(7) = 5040
fact(8) = 40320
fact(9) = 362880
fact(10) = 3628800
fact(11) = 39916800
fact(12) = 479001600
fact(13) = 6227020800
fact(14) = 87178291200
fact(15) = 1307674368000
fact(16) = 20922789888000
fact(17) = 355687428096000
fact(18) = 6402373705728000
fact(19) = 121645100408832000

`fibo(n)`

The fibonacci sequence using unsigned long. Here is the recursive definition:

fibo(0) = 0
fibo(1) = 1
fibo(n) = fibo(n - 1) + fibo(n - 2)

Note: we're using unsigned long integer, thus we should be able to compute fibo(93) which is not possible using the naive recursive version.

Running using provided tests:

shell> ./main 1 73 93
fibo(73) = 806515533049393
fibo(74) = 1304969544928657
fibo(75) = 2111485077978050
fibo(76) = 3416454622906707
fibo(77) = 5527939700884757
fibo(78) = 8944394323791464
fibo(79) = 14472334024676221
fibo(80) = 23416728348467685
fibo(81) = 37889062373143906
fibo(82) = 61305790721611591
fibo(83) = 99194853094755497
fibo(84) = 160500643816367088
fibo(85) = 259695496911122585
fibo(86) = 420196140727489673
fibo(87) = 679891637638612258
fibo(88) = 1100087778366101931
fibo(89) = 1779979416004714189
fibo(90) = 2880067194370816120
fibo(91) = 4660046610375530309
fibo(92) = 7540113804746346429
fibo(93) = 12200160415121876738

`int_sqrt(n)`

Integer part of the square root of n.

The integer square root verifies the following equations:

r = int_sqrt(n)
r * r <= n && n < (r + 1) * (r + 1)

The best algorithm for that is Heron's method (a variant of Newton's method):

let x be a first approximation of the square root such that r <= x <= n (where r is the root)
(n is a good starting value)
While x is greater than the root, replace x with the average of x and n/x:
    x = (x + n/x) / 2

Note that the root is located between x and x/n, thus we found the root when x <= n/x for the first time.

Don't forget to handle the special case for n = 0.

Running using provided tests:

shell> ./main 2 40 60
int_sqrt(40) = 6
int_sqrt(41) = 6
int_sqrt(42) = 6
int_sqrt(43) = 6
int_sqrt(44) = 6
int_sqrt(45) = 6
int_sqrt(46) = 6
int_sqrt(47) = 6
int_sqrt(48) = 6
int_sqrt(49) = 7
int_sqrt(50) = 7
int_sqrt(51) = 7
int_sqrt(52) = 7
int_sqrt(53) = 7
int_sqrt(54) = 7
int_sqrt(55) = 7
int_sqrt(56) = 7
int_sqrt(57) = 7
int_sqrt(58) = 7
int_sqrt(59) = 7
int_sqrt(60) = 7

`digit_number(n)`

The number decimal (base 10) digits in n.

Running using provided tests:

shell> ./main 3 90 110
digit_number(90) = 2
digit_number(91) = 2
digit_number(92) = 2
digit_number(93) = 2
digit_number(94) = 2
digit_number(95) = 2
digit_number(96) = 2
digit_number(97) = 2
digit_number(98) = 2
digit_number(99) = 2
digit_number(100) = 3
digit_number(101) = 3
digit_number(102) = 3
digit_number(103) = 3
digit_number(104) = 3
digit_number(105) = 3
digit_number(106) = 3
digit_number(107) = 3
digit_number(108) = 3
digit_number(109) = 3
digit_number(110) = 3

`binary_digit_number(n)`

Computes the number of binary digit (base 2) of n.

Running using provided tests:

shell> ./main 4 7 33
binary_digit_number(7) = 3
binary_digit_number(8) = 4
binary_digit_number(9) = 4
binary_digit_number(10) = 4
binary_digit_number(11) = 4
binary_digit_number(12) = 4
binary_digit_number(13) = 4
binary_digit_number(14) = 4
binary_digit_number(15) = 4
binary_digit_number(16) = 5
binary_digit_number(17) = 5
binary_digit_number(18) = 5
binary_digit_number(19) = 5
binary_digit_number(20) = 5
binary_digit_number(21) = 5
binary_digit_number(22) = 5
binary_digit_number(23) = 5
binary_digit_number(24) = 5
binary_digit_number(25) = 5
binary_digit_number(26) = 5
binary_digit_number(27) = 5
binary_digit_number(28) = 5
binary_digit_number(29) = 5
binary_digit_number(30) = 5
binary_digit_number(31) = 5
binary_digit_number(32) = 6
binary_digit_number(33) = 6

`power_of_2(n)`

Computes 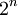$2^n$ as fast as you can (don't need to be iterative or recursive … )

Running using provided tests:

shell> ./main 5 0 32
power_of_2(0) = 1
power_of_2(1) = 2
power_of_2(2) = 4
power_of_2(3) = 8
power_of_2(4) = 16
power_of_2(5) = 32
power_of_2(6) = 64
power_of_2(7) = 128
power_of_2(8) = 256
power_of_2(9) = 512
power_of_2(10) = 1024
power_of_2(11) = 2048
power_of_2(12) = 4096
power_of_2(13) = 8192
power_of_2(14) = 16384
power_of_2(15) = 32768
power_of_2(16) = 65536
power_of_2(17) = 131072
power_of_2(18) = 262144
power_of_2(19) = 524288
power_of_2(20) = 1048576
power_of_2(21) = 2097152
power_of_2(22) = 4194304
power_of_2(23) = 8388608
power_of_2(24) = 16777216
power_of_2(25) = 33554432
power_of_2(26) = 67108864
power_of_2(27) = 134217728
power_of_2(28) = 268435456
power_of_2(29) = 536870912
power_of_2(30) = 1073741824
power_of_2(31) = 2147483648
power_of_2(32) = 4294967296

`divisor_sum(n)`

Computes the sum of the divisors of n including 1 but not n itself.

Special cases for 0 and 1 should return 1.

You can check your results with some hints: prime numbers will have a sum of 1, perfect numbers (6, 28, 496, 8128 … ) will have a sum equals to themselves.

Running using provided tests:

shell> ./main 6 0 30
divisor_sum(0) = 1
divisor_sum(1) = 1
divisor_sum(2) = 1
divisor_sum(3) = 1
divisor_sum(4) = 3
divisor_sum(5) = 1
divisor_sum(6) = 6
divisor_sum(7) = 1
divisor_sum(8) = 7
divisor_sum(9) = 4
divisor_sum(10) = 8
divisor_sum(11) = 1
divisor_sum(12) = 16
divisor_sum(13) = 1
divisor_sum(14) = 10
divisor_sum(15) = 9
divisor_sum(16) = 15
divisor_sum(17) = 1
divisor_sum(18) = 21
divisor_sum(19) = 1
divisor_sum(20) = 22
divisor_sum(21) = 11
divisor_sum(22) = 14
divisor_sum(23) = 1
divisor_sum(24) = 36
divisor_sum(25) = 6
divisor_sum(26) = 16
divisor_sum(27) = 13
divisor_sum(28) = 28
divisor_sum(29) = 1
divisor_sum(30) = 42

Testing with provided code

The provided files will help you testing your code.

The first step is to be sure (at least) that the file math_func.c compiles (you can just add a default return statement or something similar).

The files main.c describes a small program for testing your functions with some basic parameters: the function index (from 0 to 6) a min and a max value. The program will run your function with all integers from the min to the max value (included).

Here is a tiny test session (with a complete working math_func.c file):

shell> ls
AUTHORS  Makefile  main.c  math_func.c  math_func.h
shell> make
gcc -Wall -Wextra -std=c99 -pedantic -O2 -MMD  -c -o main.o main.c
gcc -Wall -Wextra -std=c99 -pedantic -O2 -MMD  -c -o math_func.o math_func.c
gcc   main.o math_func.o   -o main
shell> ./main 
main:  <op> <min> <max>
	Operators:
		0: factorial
		1: fibonacci
		2: integer square root
		3: number of digits
		4: number of binary digits
		5: power of 2
		6: sum of divisors

shell> ./main 0 0 5
fact(0) = 1
fact(1) = 1
fact(2) = 2
fact(3) = 6
fact(4) = 24
fact(5) = 120
shell> ./main 6 495 497
divisor_sum(495) = 441
divisor_sum(496) = 496
divisor_sum(497) = 79
shell> make clean
rm -f math_func.o main.o math_func.d main.d
rm -f main
shell>

20160926:Practical:C:HomeWork

Sommaire

Introduction

Code submission instructions

Archive format

Provided Files

`Makefile`

`main.c`

`math_func.h`

Task: `math_func.c`

`fact(n)`

`fibo(n)`

`int_sqrt(n)`

`digit_number(n)`

`binary_digit_number(n)`

`power_of_2(n)`

`divisor_sum(n)`

Testing with provided code

Menu de navigation

Outils personnels

Espaces de noms

Variantes

Affichages

Plus

Rechercher

Plan

Outils

20160926:Practical:C:HomeWork

Sommaire

Introduction

Code submission instructions

Archive format

Provided Files

Makefile

main.c

math_func.h

Task: math_func.c

fact(n)

fibo(n)

int_sqrt(n)

digit_number(n)

binary_digit_number(n)

power_of_2(n)

divisor_sum(n)

Testing with provided code

Menu de navigation

Rechercher

`Makefile`

`main.c`

`math_func.h`

Task: `math_func.c`

`fact(n)`

`fibo(n)`

`int_sqrt(n)`

`digit_number(n)`

`binary_digit_number(n)`

`power_of_2(n)`

`divisor_sum(n)`