20131118:TP:OCaml:Heap

Introduction

L'objectif de ce TP est d'écrire une module implémentant une structure de tas binaire [1]. Dans un premier temps le contenu (clefs et valeurs) du tas sera monomorphe, mais nous ferons en sorte dans une seconde partie de paramétré le contenu (en construisant un foncteur, que nous verrons plus tard.)

Les tas ?

Les tas sont des structures hiérarchiques (assimilables à des arbres) qui stockent un extremum (souvent un minimum, mais pas forcément) en racine de manière à le rendre rapidement accessible (la propriété s'étend sur tout l'arbre, la racine de chaque sous-arbre est un extremum pour le sous-arbre.) L'arbre est en général stocké dans un tableau et les opérations d'insertion, de suppression et de mise à jour sont en temps logarithmique.

Le principe de stockage dans un tableau est simple, la première case du tableau (d'index 0) est une sentinelle contenant un extremum absolu (souvent 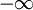$-\infty$ lorsque les clefs sont des flottants.) On trouve la racine de l'arbre en case 1 et enfin, le fils gauche du nœud i se trouvera à la case 2*i et son fils droit à la case 2*i + 1.

Le tas est un arbre parfait, par conséquent le tableau est rempli sans trou jusqu'à la case correspondant à la taille du tas.

Insertion

L'insertion est relativement simple:

1. on augmente la taille du tas
2. on ajoute la nouvelle clef à la dernière case (celle correspondant à la taille du tas)
3. ensuite on remonte cette clef jusqu'à sa vraie place, en partant de la case i:
   1. si le père (case i/2) est plus grand on l'échange avec la nouvelle clef
   2. on recommence à la case i/2, jusqu'à trouver une clef plus petite

On notera que grâce à la sentinelle, il n'est pas nécessaire de tester l'arrivée ne fin de tableau, dans le pire des cas on arrive en case 1 et on s'arrête puisque la clef de la sentinelle est forcément plus petite.

Prendre la racine

Pour la suppression, seule la suppression de la racine nous intéresse (c'est l'extremum du tas.)

Le principe est là encore relativement simple (même si l'implémentation est plus technique):

1. On remplit le trou laisser par la racine avec la dernière clef de du tas
2. On s'assure ensuite que la propriété du tas est conservé, en partant de la position i:
   1. On s'assure qu'il y a des fils
   2. Si l'un des fils est plus petit (ou plus grand le cas échéant) on échange le contenu des deux cases
   3. Si les des fils sont plus petits, on fait l'échange avec le plus petit des deux
   4. On recommence avec le fils choisi (si nécessaire.)

Mise à jour

Dans certains cas d'utilisation des tas, il est souvent nécessaire de mettre à jour la position d'une clef.

Globalement, un tas ne stock pas que des clefs, en général, on stock un couple (clef,valeur) où la clef permet de classer les valeurs stockées (typiquement dans un algo de plus courts chemins, on triera les sommets en fonctions de la distance déjà parcourue, ou en fonction d'une heuristique.)

Il est donc parfois nécessaire de changer la clef associée à une valeur. Nous ne nous intéresserons ici qu'au cas où la clef évolue vers la racine (la clef diminue ou grandit en fonction de la nature du tas.) Dans ce cas là, le principe de mise à jour est relativement simple et s'appuie sur celui de l'insertion:

1. On cherche le couple (clef,valeur) qui nous intéresse
2. On met à jour la clef
3. On applique le même principe de remontée que lors d'une insertion: on échange le contenu de la case avec celle du père si la clef de celui-ci est plus grande (ou plus petite)

Bien sûr (nous le verrons lors de l'implémentation) il faut trouver un moyen efficace de retrouver le couple dans le tas.

Implémentation

Nous allons donc implémenter ces tas. Pour ça, il nous faut décrire le type et le module que nous comptons mettre en place.

Les types

Pour le stockage du tas, nous avons besoin des types suivant:

type key = float
type value = string
 
type cell = {
  key : key;
  value : value;
}
 
type t = {
  tab : cell array;
  index : Index.t;
  mutable size : int;
  capacity : int;
}

Les types key et value servirons plus tard à paramétrer le module.

Le module Index sert à définir des index pour retrouver plus simplement les valeurs stockées (pour la mise à jour), en voici un exemple d'implémentation:

(* Module Index: index.ml *)
(* index for heap *)
 
type value = string
 
type t = (value,int) Hashtbl.t
 
let create capacity =
  Hashtbl.create capacity
 
let update k pos index =
    Hashtbl.replace index k pos
 
let remove k index =
  Hashtbl.remove index k
 
let get k index =
  Hashtbl.find index k

On ajoute également l'exception suivante (qui servira lorsque le tas est plein.)

exception Capacity_exceeded

Exercice

Votre objectif est d'implémenter le module heap.ml qui respecte l'interface suivante:

(* Heap implementation *)
 
(* Exception raised when heap is full *)
exception Capacity_exceeded
 
(* Heap content *)
type key = float
type value = string
type cell = {
  key : key;
  value : value;
}
 
(* Heap data structure *)
type t = {
  tab : cell array;
  index : Index.t;
  mutable size : int;
  capacity : int;
}
 
(* return true if the heap is empty, false otherwise *)
val is_empty : t -> bool
 
(* create cap minkey dumm:
 * create a new of capacity cap with a sentinel {minkey,dumm}
 *)
val create : int -> key -> value -> t
 
(* insert h k v
 * insert {k,v} into heap h
 *)
val insert : t -> key -> value -> unit
 
(* take_min h
 * extract minimal value (updating the whole heap) and return it
 *)
val take_min : t -> value
 
(* update h value newkey
 * find pair {oldkey, value}, replace oldkey with newkey and update
 * the heap.
 * If the pair wasn't in the heap, update acts as insert.
 *)
val update : t -> value -> key -> unit

Voici le squelette du fichier à réaliser:

(* Heap implem *)
 
exception Capacity_exceeded
 
type key = float
type value = string
 
type cell = {
  key : key;
  value : value;
}
 
type t = {
  tab : cell array;
  index : Index.t;
  mutable size : int;
  capacity : int;
}
 
let is_empty h = h.size = 0
 
let create capacity min_key dumm_val =
  {
    tab = Array.make (capacity + 1) {key=min_key;value=dumm_val};
    index = Index.create (capacity+1);
    capacity = capacity;
    size = 0;
  }
 
let insert h k v = assert false
 
let take_min h = assert false
 
let update h v newkey = assert false

Et maintenant un programme de test pour votre module:

(* Testing Heap *)
 
let h = Heap.create 256 neg_infinity ""
 
(* Build a hash table with (k,v) to be inserted (and insert them) *)
(* Store minimal key for later test *)
let minkey = ref infinity
let value_minkey = ref ""
let data =
  let _ = Random.init 42 in
  let _h = Hashtbl.create 521 in
    for i = 1 to 33 do
      let f = float (Random.int 4096) in
        minkey := min !minkey f;
        if !minkey = f then
          value_minkey := string_of_int i;
        Hashtbl.add _h (string_of_int i) f;
        Printf.eprintf "Adding: (%g,%S);" f (string_of_int i);
        if (i mod 4 = 0) then Printf.eprintf "\n%!";
        Heap.insert h f (string_of_int i);
    done;
    Printf.eprintf "\n%!";
    _h
 
(* Our main test *)
 
let main () =
  begin
    Printf.printf "take_min: %S (should be %S)\n%!"
      (Heap.take_min h) !value_minkey;
    Printf.printf "Update all reaming keys\n%!";
    Hashtbl.iter (
      fun v k ->
        Heap.update h v (float(Random.int 4096))
    ) data;
    Printf.printf "Getting all keys\n%!";
    while (not (Heap.is_empty h)) do
      Printf.printf "value: %S\n%!" (Heap.take_min h);
    done;
    Printf.printf "done\n%!";
    exit 0;
  end
 
let _ =
  try
    Printexc.record_backtrace true;
    main ();
  with
    | e ->
        Printf.eprintf "%s\n%!" (Printexc.to_string e);
        Printexc.print_backtrace stderr;
        exit 42