20141124:TP:C:BinaryTree:EN

Introduction

We'll now work with binary trees. The purpose of this session is to implement the functions declared in the file tree.h:

// Simple binary trees
 
# ifndef S3_PRACTICAL_20141124_TREE_H_
# define S3_PRACTICAL_20141124_TREE_H_
 
struct tree {
  int           key;
  struct tree  *left, *right;
};
 
/*
 * tree_compute_size(depth) compute the size of a perfect tree.
 */
static inline
size_t tree_compute_size(int depth) {
  /* FIX ME */
  return 0;
}
 
/*
 * tree_size(t) compute the size of the tree t
 */
size_t tree_size(struct tree *t);
 
/*
 * tree_height(t) compute the height of the tree t
 * Note: height of an empty tree is -1
 */
int tree_height(struct tree *t);
 
/*
 * tree_find(t, key) search for key in t
 * returns the pointer to the node holding key
 * returns NULL if not found.
 */
struct tree* tree_find(struct tree *t, int key);
 
/*
 * tree_build_regular(depth, &keys)
 * Build a perfect tree of height depth.
 * keys are set (and incremented) in infix order.
 * We first build recursively the left child (with its subtree)
 * Then we increment keys and use it to set the key of the current node
 * Finally we build recursively the right child.
 */
struct tree* tree_build_regular(int depth, int *keys);
 
/*
 * Basic printing: print the keys with a single space between each keys.
 */
 
/*
 * Depth first printing in prefix, infix or suffix order.
 */
 
void tree_depth_prefix_print(struct tree *t);
void tree_depth_infix_print(struct tree *t);
void tree_depth_suffix_print(struct tree *t);
 
/*
 * Printing using a breadth first traversal
 * Keys are separated by space
 * Each level are separated by a new-line.
 */
void tree_breadth_print(struct tree *t);
 
/*
 * dot output (see the subject)
 */
void tree_dot_out(struct tree *t, char *fname);
 
# endif /* S3_PRACTICAL_20141124_TREE_H_ */

• Implement the static function tree_compute_size(depth) that compute the size of a perfect tree (all internal nodes have 2 child, all leaves are on the same level) also known as arbre complet in french.

For the rest of the practical session you'll implement all these functions in the file tree.c.

Basic operations

The first step is to implement classic operations on binary trees. We recall definitions:

Size: the number of nodes in the tree.

Height: the depth of a tree, defined recursively using: empty tree has a height of -1, a leaf has a height of 0 and the height of an internal node is the max of the height of its children plus one.

• Implement all basic operations (size, height and find)

Building a Tree

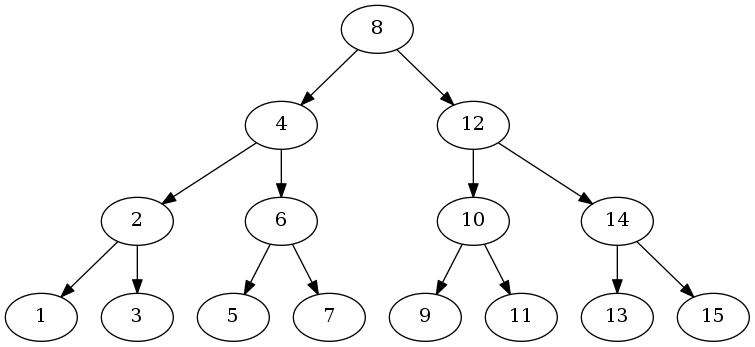
In order to test our functions, we need a function to build a tree. We want simple tree with a known form, the next figure shows a tree of depth 3:

This tree can build using the following strategy:

• If depth is -1 we return an empty node (NULL)
• Otherwise:
  • We build the left child recursively (with depth - 1)
  • We increment *keys and set the key of the current node
  • We build the right child recursively (with depth - 1)

If keys points to an int initialized at 0, we obtain a tree where keys are sorted in infix order like in the previous figure.

• Implement the function tree_build_regular(depth, &keys)

Printing

We now want to print the keys of a tree using various traversal.

Depth First

For the depth first traversal, we want a basic sequential printing, with output looking like that (on the tree of the previous figure):

Prefix:
8 4 2 1 3 6 5 7 12 10 9 11 14 13 15 

Infix:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 

Suffix
1 3 2 5 7 6 4 9 11 10 13 15 14 12 8 

• Implement the following functions: tree_depth_prefix_print(t), tree_depth_infix_print(t) and tree_depth_suffix_print(t)

Breadth First

For the breadth first printing, you'll need a queue. If you haven't done it before, you need to implement, at least, the following functions:

struct queue {
  void         *val;
  struct queue *next;
};
 
static inline
struct queue* queue_empty() { return NULL; }
static inline
int queue_is_empty(struct queue *q) { return q == NULL; }
 
void queue_push(struct queue **q, void *p) {
  /* FIX ME */
}
 
void* queue_pop(struct queue **q) {
  /* FIX ME */
}

Remember: a queue is a circular simply linked list where the entry point is the most recent element in the queue and its next element the least recent (the top) of the queue.

You'll also need queue for the next exercise.

• Implement the queue data structure.
• Implement the function tree_breadth_print(t)

Output in the dot format

The purpose of this question is to use dot to build a visual representation of our trees. The next subsections explains details on the format and how to manipulate files.

• Implement the function tree_dot_out(t, fname) that output the tree t in the file named fname.

The dot format

Graphviz [1], often refered as dot, is a usefull graph (and trees) visualization tool. Graphs are represented using a simple format and then can be transformed into image using various algorithm. For trees, the best tools is probably dot (but you can try fdp, sfdp, circo, neato or twopi.)

For example, the tree in the previous figure was obtained from this file:

digraph Tree {
  8 -> 4;
  8 -> 12;
  4 -> 2;
  4 -> 6;
  12 -> 10;
  12 -> 14;
  2 -> 1;
  2 -> 3;
  6 -> 5;
  6 -> 7;
  10 -> 9;
  10 -> 11;
  14 -> 13;
  14 -> 15;
}

digraph indicates that we want a directed graph (better for a tree), Tree is name given to our graph and can be replaced by any valid identifier, we can then list the edges of the tree in the form: parent -> child;.

dot layout algorithm requires that we list edges from the top of the tree to its bottom (otherwise the output may not be like we expect.) The best result is obtained from breadth first print of the edges.

The previous image was generated using the previous file (named tree.dot) with this command:

shell> ls
tree.dot
shell> dot -Tpng tree.dot -O
shell> ls
tree.dot   tree.dot.png

Files I/O

We want to output our format in a file, for that, we'll use features from <stdio.h>, here is the base code for opening (with error management) of the file:

void tree_dot_out(struct tree *t, char *fname) {
  if (t) {
    FILE               *file;
    // open file in create/replace mode
    if ( (file = fopen(fname, "w")) == NULL) {
      err(3, "Error while creating %s", fname);
    }
 
    fprintf(file, "digraph Tree {\n");
 
    /* BFS printing of tree edges */
    /* FIX ME */
 
    fprintf(file, "}\n");
    // close the file
    fclose(file);
  }
}

The function fprintf(file, format, ... ) is similar to printf(3), but rather than printing of the standard output, we print to the given file.

Testing

Once your file tree.c is complete, you can use the following main file to test it:

// testing.c
// Testing trees
 
# include <assert.h>
# include <stdio.h>
# include <stdlib.h>
# include <time.h>
 
# include "tree.h"
 
static inline
char* build_fname() {
  char         *fname;
  fname = calloc(30, 1);
  time_t        t;
  t = time(NULL);
  strftime(fname, 30, "tree-%F-%H-%M-%S.dot", localtime(&t));
  return fname;
}
 
void tests(int depth) {
  struct tree          *t = NULL;
 
  // Empty cases
  assert(tree_size(t) == 0);
  assert(tree_height(t) == -1);
  assert(tree_find(t, 1) == NULL);
 
  // build a tree
  int                   key = 0;
  t = tree_build_regular(depth, &key);
  assert(tree_height(t) == depth);
  assert(tree_size(t) == tree_compute_size(depth));
  {
    // searching
    struct tree        *r;
    assert(tree_find(t, t->key) == t);
    assert( (r = tree_find(t, 1)) != NULL && r->key == 1);
    assert( (r = tree_find(t, key - 1)) != NULL && r->key == key - 1);
    assert( (r = tree_find(t, key + 1)) == NULL);
  }
 
  // Printing
  printf("Prefix:\n");
  tree_depth_prefix_print(t);
  printf("\n\nInfix:\n");
  tree_depth_infix_print(t);
  printf("\n\nSuffix\n");
  tree_depth_suffix_print(t);
  printf("\n");
 
  printf("\nBFS:\n");
  tree_breadth_print(t);
 
  // Dot output
  char                 *fname;
  fname = build_fname();
  printf("Dot file: %s\n", fname);
  tree_dot_out(t, fname);
}
 
int main(int argc, char *argv[]) {
  int           depth = 3;
  if (argc > 1)
    depth = strtol(argv[1], NULL, 10);
 
  tests(depth);
 
  return 0;
}

BONUS: Tree Iterators

We now want to implement a mechanism of iterator on tree. Remember, an iterator is an abstract data that provides a simple way to access values stored in a container one by one, without knowing the inner structure.

The provided operations are:

/*
 * tree_iterator(t) returns an iterator on t
 */
struct iterator* tree_iterator(struct tree *t);
 
/*
 * iterator_next(it) move to next element
 * if it is not the end of the iteration
 */
void iterator_next(struct iterator *it);
/*
 * iterator_is_end(it) returns true if it is the end of the iteration
 */
int  iterator_is_end(struct iterator *it);
 
/*
 * iterator_get(it) returns the key of the current node
 * undefined if it is the end
 */
int iterator_get(struct iterator *it);

We need to choose the order of iteration. In our case, the simplest solution is to use a breadth first iteration. Thus the implementation of the iterator structure looks like this:

struct iterator {
  struct tree          *cur;
  struct queue         *q;
};

Here are the guidelines to implement these iterators:

• At the begining, you should put the root in the cur field and push its children (beware of empty nodes.)
• When calling next, you should pop the next element out of the queue (if not empty) and push its children.
• The iterator is finished (it is the end iterator) when no more nodes are available, meaning that the queue was empty when you've done the last call to next.
• The iterator of an empty tree is directly the end iterator.