20140922:TP:C:Introduction:EN

 La version française se trouve ici: 20140922:TP:C:Introduction

First Pratical Session

This session is an initiation, its goal is to introduce basic C notions.

Compile and Makefile

First Program

Now, we'll see how to compile a C program.

We start with a simple program: Hello World

/* hello_world.c: Hello World ! */
 
// Includes:
 
// standard lib, always there
#include <stdlib.h>
 
// standard I/O needed for printf
#include <stdio.h>
 
// Main function
int main()
{
  // The dummiest example
  printf("Hello World !\n");
 
  // always return something
  // 0 is success
  return 0;
}

Type this piece of code into a file named hello_world.c. In order to compile it, you can choose gcc or clang.

> ls
hello_world.c
> clang hello_world.c
> ls
a.out  hello_world.c

Without options, almost all Unix compilers will produce a binary file called a.out. In order to choose a name, we use the option -o followed by the name you want. But, we won't stop there: we add all the options that we'll use everytime we want to compile a file:

• -Wall activates all classical warnings.
• -Wextra activates extra warnings.
• -Werror warnings must be treated as errors.
• -std=c99 we're using C99 standard.
• -O2 second level of optimization (add more warnings.)

Our command line is now:

> rm a.out
> clang -Wall -Wextra -std=c99 -O2 hello_world.c -o hello_world
> ls
hello_world   hello_world.c

Choosing our compiler: the 2 available compilers produce binary programs slightly equivalent with the same set of options. But, their error messages are different. Let's test it: remove a semi-colon (;) somewhere in your file, compile it with both compilers and compare the messages !

Make and Implicit Rules

The make command is able to automatically produce a binary file out-of a C file without any specific Makefile:

> rm hell_world
> make hello_world
cc     hello_world.c   -o hello_world

That's convenient, but we don't have our options et and we can't choose the compiler. Fortunately for us, the automatic rules used by make can be parameterized using envirronment variables that can be set in the shell or in a Makefile.

Here is a simple Makefile that set usefull variables for compiling single C files, read and try it:

# Makefile with basic concepts
 
# Define compiler and options
CC=clang
CFLAGS= -Wall -Wextra -std=c99 -O2
 
# avoid calling make without target
# ONLY FOR THIS EXERCICE
all:
	@echo "*** NO DEFAULT RULES ***"
	@false
 
clean::
	rm -f *~ *.o
 
# END (do not delete)

Some tests:

> rm -f hello_world
> make hello_world
clang -Wall -Wextra -std=c99 -O2    hello_world.c   -o hello_world
> make hello_world.o
clang -Wall -Wextra -std=c99 -O2   -c -o hello_world.o hello_world.c

The last command shows us that we can produce .o files directly.

Options, Headers, Manual Pages

This exercise is here to let you learn howto use manual pages to find standard headers needed in your code.

Headers have been removed from this file, use man to find-out the missing lines:

/* A little example with includes */
 
/*
 * Goals:
 * * understand include strategy
 * * read man pages for function
 */
 
 
// add here missing includes
 
const int LIMITS[] =
  {
    RLIMIT_CORE,
    RLIMIT_CPU,
    RLIMIT_DATA,
    RLIMIT_FSIZE,
    RLIMIT_NOFILE,
    RLIMIT_STACK,
    RLIMIT_AS
  };
 
const char *LIMIT_NAME[] =
  {
    "RLIMIT_CORE",
    "RLIMIT_CPU",
    "RLIMIT_DATA",
    "RLIMIT_FSIZE",
    "RLIMIT_NOFILE",
    "RLIMIT_STACK",
    "RLIMIT_AS"
  };
 
void print_limit(const char *name, const struct rlimit *rlp)
{
  printf("%s: ",name);
  if (rlp->rlim_cur == RLIM_INFINITY)
    printf("unlimited");
  else
    printf("%lu",rlp->rlim_cur);
  if (rlp->rlim_max == RLIM_INFINITY)
    printf(" unlimited\n");
  else
    printf(" %lu\n",rlp->rlim_cur);
}
 
int main()
{
  struct rlimit         rlp;
  printf("break address: %p\n", sbrk(0));
  for (size_t i=0; i < sizeof (LIMITS) / sizeof (int); ++i)
    {
      if (getrlimit(LIMITS[i], &rlp) < 0)
        {
          perror("getrlimit failed");
          return 2;
        }
      print_limit(LIMIT_NAME[i], &rlp);
    }
  return 0;
}

You should start by looking at manual pages for the various functions appearing in the program (don't try to compile it, you'll only get a huge amount of errors.)

Here is a quick lists of functions you should try: getrlimit(3), printf(3) et sbrk(2) (do it in order, the first function's manual page may help you remove a lot of errors.)

Programm Command Line

Acces the Command Line

The programm command line (options passed when run) can be accessed using parameters of the main function:

int main(int argc, char *argv[])
{
  // do your job here
  // always return some int
  return 0;
}

• argc is the size of the array of parameters
• argv is the array of parameters, note that there's always an entry in it: your program name in the first cell (0.)

Now, you should try to write the program that has the following output:

> ./args a b c d e
argv[0] = "./args"
argv[1] = "a"
argv[2] = "b"
argv[3] = "c"
argv[4] = "d"
argv[5] = "e"

In order to obtain each line, you can use printf with following format string "argv[%d] = \"%s\"\n"

Basic Usage of Command Line

In the following, we'll code several arithmetic functions that we want to test easily. Our goal is to use arguments on the command line (when they are present) or (when no arguments are provided) some predefined default values.

• Write to some program that compute the sum of two number x and y provided as arguments on the command line. If only one argument is provided, your program will set y 22 and if no arguments are provided it will set x to 20.

Example:

> ./simple
20 + 22 = 42
> ./simple 1
1 + 22 = 23
> ./simple 21 21
21 + 21 = 42

You'll need the function atoi(3) in order to convert strings into integer.

Arithmetics

We'll now write a series of classical arithmetics functions. You will put all these functions in a unique file called simple_math.c which will be used later in global program.

While coding the following functions, use the previous question to write small test programs. You can also use assert(3) (check the man page.)

Factorial

The classical recursive function. You can either write an iterative or a recursive function.

/*
 * fact(n) compute n!
 * fact(0) returns 1
 */
unsigned fact(unsigned n);

You don't need to manage negative number, we're working with unsigned integer.

Fibonacci

Classical Fibonacci sequence, note that we're using the one defined with: fibo(0) == 0,fibo(1) == 1 et fibo(n) = fibo(n-1) + fibo(n-2). Here again you can write recursive or iterative version, or if you remeber how it works the linear recursive version.

/*
 * fibo(n) compute the n-th term of Fibonacci sequence
 * fibo(0) returns 0
 * fibo(1) returns 1
 */
unsigned fibo(unsigned n);

Power

Another classic: $a^b$ (where a and b are integers.)

Of course, you should try to write the quick exponential algorithm based on $a^{2\times n} = \left(a^2\right)^{n}$. Try to wrote the iterative version, it's a good exercise.

/*
 * power(a, b) computes a power b
 */
unsigned power(unsigned a, unsigned b);

Eratosthene sieve

Our goal is to display every prime number smaller that n.

For this algorithm, we need an array of n+1 cells indicating (at after the execution) whether i is prime or not. At the begining, every all numbers are considered prime. Since we don't have any boolean type, we'll use un array of unsigned 8 bits integer, defined this way:

  // n is our parameter
  uint8_t *prime;
  prime = malloc(n+1);

We then iterate from i=2 to i=n, if i is marked has being prime, we print it and enter the second loop, otherwise we continue on the next value. The second loop marks every multiple of the current i has being not prime.

Remarks:

• We can stop the outer loop at $\sqrt n$ (the rest of the array is correctly filled) but since we want to print them, we can continue until the end of the array.
• In order to mark every multiple of i, we can observe:
  • every multiple smaller than $i^2$ are already marked
  • all other multiple are of the form $i^2 + i*j$ with j from 0 to i^2 + i*j reach n.

For the display, start with one number per line, then try to do something like this:

002 003 005 007 011 013 017 019 023 029 031 037 041 043 047 053 059 061 067 
071 073 079 083 089 097 101 103 107 109 113 127 131 137 139 149 151 157 163 
167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 
271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 
389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499

To get that kind of output, you need to play around integer alignement in printf(3) and its return value in order to detect when to push a new line.

// prime(n) print all prime number between 2 and n
void prime(unsigned n);

Square root

As a starting point, we'll compute the integer part the square root. We'll use Heron method (a special case of the Newton's method.)

It's an approximation based algorithm. We start with a given approximation x such that 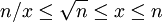$n/x \leq \sqrt n \leq x \leq n$.

We'll now narrow the range between x and n/x to get closer to the root. The best candidat as the new approximation is the mean between x and n/x. Since we want the integer part of the root, we can stop the algorithm as soon as x <= n/x (range boundary are swept.)

The initial approximation value is not really important as long as it respect the initial inequation. We thus can choose n as our first x (better first approximation yeild better performances.) Beware to directly trap input values 0 or 1 to avoid computation issues.

Implement the following function:

/*
 * integer_sqrt(n) returns the integer part of the square root of n.
 */
unsigned integer_sqrt(unsigned n);

You can test your function by:

• producing a serie of random values n and checking that integer_sqrt(n*n) == n
• producing a serie of random values n and checking that x * x <= n && n < (x + 1) * (x + 1) with x = integer_sqrt(n)

We now switch to floating point numbers. The algorithm is the same, but this time we don't need the constraint of the majoring approximation et choose to stop the algorithm when the distance between x and n/x is below an arbitrary threshold (we can take 1e-6 for example.

In order to write you function, you may need a min on floating point number. You can implement this function marked as static inline.

static inline
double dmin(double a, double b) { return a<b?a:b; }

Now, it's your turn !

/*
 * double_sqrt(n) Compute the square root of n
 */
double double_sqrt(unsigned n);

Of course, you must not use the libc's sqrt(3) function, but you may need functions like abs(3) from math.h. Beware, at compile time, you'll need to add the library m (take a look at the Makefile.)

Putting everything together

In order to finish, we'll gather all these functions into a single program and use the command line to choose which function to call.

More than one file

All our functions are in a file simple_math.c, we need to write an header for it, called: simple_math.h

You'll gather function prototypes (given in the subject) into the header file.

We then have to protect the header against multiple inclusion. The official recommandation are: we use the pre-processor. We use a name to mark the header:

#ifndef SIMPLE_MATH_H_
#define SIMPLE_MATH_H_
 
/* Prototypes go here */
 
#endif

To compile the final program, we need to compile separately the file simple_math.c in order to obtain the file simple_math.o (make is here to help.)

The Main Program

Our main program will use the command line to select which functions to call. Let's keep it simple: the first parameter will be an integer selecting the function to call. The other parameters will serve as parameters for the called function.

In the following table, we describe meaning of parameters and default values to be tested:

0	fact	One parameter, default value 5
1	fibo	One parameter, default value 7
2	power	Two parameters, default values 2 and 16
3	prime	One parameter, default value 500
4	sqrt	One parameter, default value 200
5	double_sqrt	One parameter, default value 200

Use the previous exercise to see how to manage default values.

If there's no parameter, you must quit the program with an error message of your choice and a return value (in main) of 1.

If there's at least one parameter, but the first one doesn't match any function of the list, you must quit with an error message and a return value of 2.

Files

• Makefile
• simple_math.c
• simple_math.h
• main.c

# Simple Makefile
# Practical session 01
 
# Global Compilation Variables
 
# The compiler
CC=clang
 
# Pre-processor flags
CPPFLAGS=
 
# C compiler flags
CFLAGS= -Wall -Wextra -Werror -std=c99 -O3
 
# Linker flags
LDFLAGS=
 
# Linker libs
LDLIBS= -lm
 
# all target just call the production of main
all: main
 
# main target using implicit rules, just express dependencies
main: main.o simple_math.o
 
# clean compilation products
clean:
	rm -f *~ *.o
	rm main
 
# END of File