20151207:TP:C:Graph

De wiki-prog
Révision de 7 décembre 2015 à 09:22 par Slashvar (discuter | contributions) (→‎Testing with huge graph)

(diff) ← Version précédente | Voir la version courante (diff) | Version suivante → (diff)
Aller à : navigation, rechercher


Introduction

The purpose of this practical session is to implement some graph algorithms. We work here with undirected and unweighted graphs.

Graph representation

We adopt a compact version of the adjacency list representation (the dynamic version in your algorithm tutorial) based on vector (list implemented with dynamic arrays.)

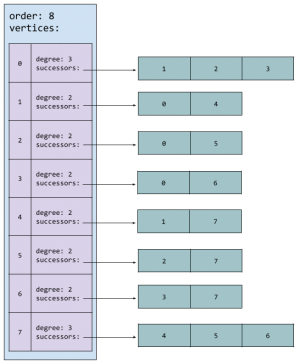
The data structure is pretty straightforward, since we have the simplest form of graph (no cost, only successors, no predecessors, single links … ) We have a main structure containing the order of the graph and a vertex array, each vertex contains its degree and an array of successors. Vertex identifiers start at 0 (so no black magic is required to find a vertex in the graph … )

The following figures show a graph and its representation.

A graph
Representing the graph

The type and the provided tools follow:

The header: 

/* graph.h: Simple Graph implementation */
 
# ifndef S3_PRACTICAL_GRAPH_H_
# define S3_PRACTICAL_GRAPH_H_
 
# include <stdlib.h>
 
struct vertex {
  size_t       degree;
  unsigned    *succ;
};
 
struct graph {
  unsigned             order;
  struct vertex       *vertices;
};
 
/* new_graph(order) create an empty (no link) graph */
/* order: number of vertices */
struct graph* new_graph(unsigned order);
 
/* graph_set_max_degree(g, vertex, degree) pre-allocate vertex's successors
 * array for the given degree, vertex degree field is set to 0. */
void graph_set_max_degree(struct graph *g, unsigned vertex, size_t degree);
 
/* graph_add_edge(g, v0, v1) add an edge between v0 and v1 */
/* max degree must have been set for both vertices */
/* edges are undirected and successors must be added to both v0 and v1 */
void graph_add_edge(struct graph *g, unsigned v0, unsigned v1);
 
 
/* graph_delete(g) delete and release g */
void graph_delete(struct graph *g);
 
/* foreach macro for successors */
/* s_name_ must be a predeclared var of type unsigned* */
# define for_successors(g_, v_, s_name_)                             \
  for (s_name_ = (g_)->vertices[v_].succ;                            \
      s_name_ < (g_)->vertices[v_].succ + (g_)->vertices[v_].degree; \
      s_name_++ )
 
# endif /* S3_PRACTICAL_GRAPH_H_ */

The source code: 

/* graph.c: Simple Graph implementation */
 
# include <stdlib.h>
 
# include "graph.h"
 
/* new_graph(order) create an empty (no link) graph */
/* order: number of vertices */
struct graph* new_graph(unsigned order) {
  struct graph *g = malloc(sizeof (struct graph));
  g->order = order;
  g->vertices = calloc(order, sizeof (struct vertex));
  return g;
}
 
/* graph_set_max_degree(g, vertex, degree) pre-allocate vertex's successors
 * array for the given degree, vertex degree field is set to 0. */
void graph_set_max_degree(struct graph *g, unsigned vertex, size_t degree) {
  struct vertex *v = g->vertices + vertex;
  v->succ = calloc(degree, sizeof (unsigned));
  v->degree = 0;
}
 
/* graph_add_edge(g, v0, v1) add an edge between v0 and v1 */
/* max degree must have been set for both vertices */
/* edges are undirected and successors must be added to both v0 and v1 */
void graph_add_edge(struct graph *g, unsigned v0, unsigned v1) {
  struct vertex *pv0 = g->vertices + v0;
  struct vertex *pv1 = g->vertices + v1;
  pv0->succ[pv0->degree] = v1;
  pv0->degree += 1;
  pv1->succ[pv1->degree] = v0;
  pv1->degree += 1;
}
 
void graph_delete(struct graph *g) {
  for (unsigned i = 0; i < g->order; i++) {
    struct vertex *v = g->vertices + i;
    free(v->succ);
  }
  free(g->vertices);
  free(g);
}

Reading and manipulating the graph

The purpose here is to correctly manipulate the graph representation.

Provided code: reading NDE file

The file format NDE (Nodes Degree Edges) provides an easy to read format for undirected/unweighted graph. It's a text format, composed as follow:

  • a first line with a single integer representing the order of the graph
  • order lines containing 2 integers: the vertex id and its degree
  • a serie of lines containing 2 integers representing each edge

The graph in the previous figure is represented by the file: 

8
0 3
1 2
2 2
3 2
4 2
5 2
6 2
7 3
0 1
0 2
0 3
1 4
2 5
3 6
4 7
5 7
6 7

Vertex id start at 0 and each edge appears only once.

I provide tools to read the format:

The header: 

/* reader.h : Reading graph out of NDE format */
 
# ifndef S3_PRACTICAL_READER_H_
# define S3_PRACTICAL_READER_H_
 
# include "graph.h"
 
struct graph* read_graph(const char *fname);
 
# endif /* S3_PRACTICAL_READER_H_ */

And the code: 

/* reader.c: Reading graph out of NDE format */
 
# include <assert.h>
# include <err.h>
# include <stdio.h>
# include <stdlib.h>
# include <string.h>
 
# include "graph.h"
# include "reader.h"
 
static inline
size_t read_order(FILE *fin) {
  unsigned      order;
  if (fscanf(fin, "%u\n", &order) != 1)
    errx(3, "Unable to read order");
  return order;
}
 
static inline
void read_degrees(FILE *fin, struct graph *g) {
  for (size_t c = 0; c < g->order; ++c) {
    unsigned    v, d;
    if (fscanf(fin, "%u %u\n", &v, &d) != 2)
      errx(3, "Unable to read degree");
    graph_set_max_degree(g, v, d);
  }
}
 
static inline
void read_edges(FILE *fin, struct graph *g) {
  for (;;) {
    unsigned    s,d;
    if (fscanf(fin, "%u %u\n", &s, &d) != 2)
      break;
    graph_add_edge(g, s, d);
  }
}
 
struct graph* read_graph(const char *fname) {
  struct graph *g = NULL;
  FILE         *fin;
  fin = fopen(fname, "r");
  if (fin == NULL)
    err(3, "Error opening %s", fname);
  g = new_graph(read_order(fin));
  read_degrees(fin, g);
  read_edges(fin, g);
  fclose(fin);
  return g;
}

Printing dot representation

Goal: output a dot representation of the graph.

We want to build a dot representation of the graph. The output for the example graph used so far should looks like: 

graph G {
  0 -- 1;
  0 -- 2;
  0 -- 3;
  1 -- 4;
  2 -- 5;
  3 -- 6;
  4 -- 7;
  5 -- 7;
  6 -- 7;
}
  • Complete the file dot_output.c:

The header file: 

/* dot_output.h: write graph in dot format */
 
# ifndef S3_PRACTICAL_DOT_OUTPUT_H_
# define S3_PRACTICAL_DOT_OUTPUT_H_
 
# include "graph.h"
 
void dot_output(const char *fname, struct graph *g);
 
# endif /* S3_PRACTICAL_DOT_OUTPUT_H_ */

The file you need to complete: 

/* dot_output.c: write graph in dot format */
 
# include <err.h>
# include <stdio.h>
# include <stdlib.h>
 
# include "dot_output.h"
# include "graph.h"
 
void dot_output(const char *fname, struct graph *g) {
  FILE *file;
  file = fopen(fname, "w");
  if (file == NULL) {
    warn("can't open %s", fname);
    return;
  }
  /**********/
  /* FIX ME */
  /**********/
  fclose(file);
}

Depth First

Goal: DFS algorithm that prints the spanning tree and add the backward edges.

Printing helper

Here are some code to print the spanning tree in dot: 

/* spanning_tree_print.h: tools for spanning tree display */
 
# ifndef S3_PRACTICAL_SPANNING_TREE_PRINT_H_
# define S3_PRACTICAL_SPANNING_TREE_PRINT_H_
 
# include <err.h>
# include <stdio.h>
# include <stdlib.h>
 
static FILE *target_file = NULL;
 
/* open and initilize spanning tree output */
static inline
int init_spanning_output(const char *fname) {
  if (target_file != NULL) {
    warnx("an output file is already opened");
    return 0;
  }
  target_file = fopen(fname, "w");
  if (target_file == NULL) {
    warnx("can't open output file %s", fname);
    return 0;
  }
  fprintf(target_file, "digraph Spanning {\n");
  return 1;
}
 
/* finish and close spanning tree output */
static inline
int close_spanning_output() {
  if (target_file == NULL) {
    warnx("can't close not opened output file");
    return 0;
  }
  fprintf(target_file, "}\n");
  fclose(target_file);
  target_file = NULL;
  return 1;
}
 
/* print discovery edge */
static inline
void print_discovery(unsigned s, unsigned d) {
  if (target_file)
    fprintf(target_file, "  %u -> %u;\n", s, d);
}
 
/* print backward edge */
static inline
void print_backward(unsigned s, unsigned d) {
  if (target_file)
    fprintf(target_file, "  %u -> %u [constraint=false color=red];\n", s, d);
}
 
# endif /* S3_PRACTICAL_SPANNING_TREE_PRINT_H_ */

The algorithm

We perform a traditional DFS using a calling function and its recursive sub-function. Marking of vertices is done using pre-order numbering.

In order to correctly detect backward edges, we use parent information and pre-order numbering. An edge u -- v is backward if:

  • v is marked (so u -- v is not a discovery edge)
  • v is not the parent of u in the traversal
  • pre[v] < pre[u] (pre contains pre-order numbering.)

The last condition ensures that we only print each backward edge once.

The DFS must be complete (we visit all vertices, even if the graph is not connected) and have a starting point.

Here is the header file: 

/* dfs_spanning_tree.h: building DFS spanning tree */
 
# ifndef S3_PRACTICAL_DFS_SPANNING_TREE_TREE_H_
# define S3_PRACTICAL_DFS_SPANNING_TREE_TREE_H_
 
# include "graph.h"
 
void dfs(struct graph *s, unsigned src);
 
# endif /* S3_PRACTICAL_DFS_SPANNING_TREE_TREE_H_ */

The recursive function will have the following prototype: 

void dfs_rec(struct graph *g, unsigned v, unsigned p, unsigned pre[], unsigned *c);

Parameters have the following meaning:

  • g: the graph
  • v: the current vertex
  • p: parent of the current vertex in the spanning tree
  • pre: vector of pre-order numbering
  • c: pointer to the counter for pre-order numbering (address passing)

The calling function will: initialize the counter and the pre-order vector, start the algorithm on src and restarts it on unseen vertices to obtain a full DFS.

  • Implement the DFS.

Breadth first and maximal distance

We know implement a BFS that will compute the eccentricity of its starting vertex (maximal length of elementary paths starting on the given vertex.)

Queue implementation

The following header contains a basic queue implementation: 

/* basic int queue implementation */
 
# ifndef S3_PRACTICAL_GRAPH_QUEUE_H
# define S3_PRACTICAL_GRAPH_QUEUE_H
 
# include <assert.h>
# include <stdlib.h>
 
struct qcell {
  struct qcell *next;
  unsigned      val;
};
 
/* queue sentinel */
struct queue {
  struct qcell *entry;
};
 
static inline
struct queue* new_queue() {
  return calloc(1, sizeof (struct queue));
}
 
static inline
int queue_is_empty(struct queue *queue) {
  return queue->entry == NULL;
}
 
static inline
void queue_push(struct queue *queue, unsigned x) {
  struct qcell *tmp = malloc(sizeof (struct qcell));
  tmp->val = x;
  tmp->next = tmp;
  if (queue->entry) {
    tmp->next = queue->entry->next;
    queue->entry->next = tmp;
  }
  queue->entry = tmp;
}
 
static inline
unsigned queue_pop(struct queue *queue) {
  assert(queue->entry);
  struct qcell *tmp = queue->entry->next;
  unsigned r = tmp->val;
  if (tmp->next == tmp)
    queue->entry = NULL;
  else
    queue->entry->next = tmp->next;
  free(tmp);
  return r;
}
 
# endif

Operation's names are self describing.

The algorithm

Here is a description of the BFS algorithm that compute the eccentricity: 

simple_bfs(g, src):
  dist: size_t vector of length g->order initialized to (g->order + 1)
  q: new empty queue
  last: vertex id
  last = src
  dist[src] = 0
  push src in q
  do:
    v = pop next value in q
    last = v
    for successors s of v:
      if dist[s] > g->order:
        dist[s] = dist[v] + 1
        push s in q
  while q is not empty
  return dist[last]

The header for the BFS: 

/* bfs.h: BFS traversal computing maximal distance */
 
# ifndef S3_PRACTICAL_BFS_H_
# define S3_PRACTICAL_BFS_H_
 
# include <stdlib.h>
 
# include "graph.h"
 
size_t simple_bfs(struct graph *g, unsigned src);
 
# endif /* S3_PRACTICAL_BFS_H_ */
  • Implement the function simple_bfs(g, src)

Testing

In order to test your code, here is a simple main file: 

/* Some tests */
 
# include <assert.h>
# include <err.h>
# include <stdio.h>
# include <stdlib.h>
 
# include "bfs.h"
# include "dfs_spanning_tree.h"
# include "dot_output.h"
# include "graph.h"
# include "reader.h"
 
void basic_test(const char *fname, const char *fname_out) {
  struct graph *g;
  g = read_graph(fname);
  if (g == NULL)
    errx(3, "Error while opening file %s", fname);
  printf("Graph order: %u\n", g->order);
  dot_output(fname_out, g);
  dfs(g, 0);
  size_t maxdist;
  maxdist = simple_bfs(g, 0);
  printf("Maximal distance from 0: %zu\n", maxdist);
  graph_delete(g);
}
 
int main(int argc, char *argv[]) {
  if (argc < 3)
    errx(1, "missing arguments");
  basic_test(argv[1], argv[2]);
  return 0;
}

And a simple Makefile: 

# Makefile
 
CC=clang -fsanitize=address
CPPFLAGS= -MMD
CFLAGS= -Wall -Wextra -std=c99 -O2
LDFLAGS=
LDLIBS=
 
SRC= main.c graph.c dot_output.c reader.c dfs_spanning_tree.c bfs.c
OBJ= ${SRC:.c=.o}
DEP= ${SRC:.c=.d}
 
main: ${OBJ}
 
-include ${DEP}
 
.PHONY: clean
 
clean:
	rm -f ${OBJ} ${DEP}
	rm -f main
 
# END


Testing with huge graph

While the DFS (being recursive) can't handle huge graph (more 100k vertices), the BFS should works on them. In the same spirit displaying with dot huge graph is useless and probably unreadable. Thus, you can build a simple test file in order to test your BFS on bigger graphs.

Here is a modification of the previous main for that: 

/* Some tests */
 
# include <assert.h>
# include <err.h>
# include <stdio.h>
# include <stdlib.h>
 
# include "bfs.h"
# include "dfs_spanning_tree.h"
# include "dot_output.h"
# include "graph.h"
# include "reader.h"
 
void basic_test(const char *fname, const char *fname_out) {
  struct graph *g;
  g = read_graph(fname);
  if (g == NULL)
    errx(3, "Error while opening file %s", fname);
  printf("Graph order: %u\n", g->order);
  dot_output(fname_out, g);
  dfs(g, 0);
  size_t maxdist;
  maxdist = simple_bfs(g, 0);
  printf("Maximal distance from 0: %zu\n", maxdist);
  graph_delete(g);
}
 
void huge_graph_test(const char *fname) {
  struct graph *g;
  g = read_graph(fname);
  if (g == NULL)
    errx(3, "Error while opening file %s", fname);
  printf("Graph order: %u\n", g->order);
  size_t maxdist;
  maxdist = simple_bfs(g, 0);
  printf("Maximal distance from 0: %zu\n", maxdist);
  graph_delete(g);
}
 
int main(int argc, char *argv[]) {
  if (argc < 2)
    errx(1, "missing arguments");
  if (argc > 2)
    basic_test(argv[1], argv[2]);
  else
    huge_graph_test(argv[1]);
  return 0;
}

With this version, if you provide 2 file names, it'll behave just like previously, otherwise with just a single file name, it'll do only the BFS.

If you want to try your BFS on really huge graph, here are some files:

  • fe_pwt.nde [1] (1.9MB, 36463 vertices)
  • ip.nde [2] (263MB, 2250046 vertices)
  • roadNet-PA.nde [3] (29MB, 1087562 vertices)

Here are some results with these files: 

shell> /usr/bin/time -p ./main fe_pwt.nde 
Graph order: 36463
Maximal distance from 0: 261
real 0.13
user 0.12
sys 0.00
shell> /usr/bin/time -p ./main ip.nde 
Graph order: 2250046
Maximal distance from 0: 8
real 9.93
user 9.72
sys 0.21
shell> /usr/bin/time -p ./main roadNet-PA.nde 
Graph order: 1087562
Maximal distance from 0: 599
real 1.42
user 1.37
sys 0.04
Récupérée de « http://wiki-prog.infoprepa.epita.fr/index.php?title=20151207:TP:C:Graph&oldid=3304 »