20140922:TP:C:Introduction

 English version is here: 20140922:TP:C:Introduction:EN

Premier TP

Ce TP est une initiation et a pour but de vous faire mettre en pratique les premières notions de C que nous avons vu ce matin. Le TP est volontairement long, afin de donner du travail à tout le monde.

Compilation et Makefile

Premier programme

Nous allons maintenant voir comment compiler un premier programme en C.

Pour ça nous allons utiliser ce qu'il y a de plus simple: Hello World

/* hello_world.c: Hello World ! */
 
// Includes:
 
// standard lib, always there
#include <stdlib.h>
 
// standard I/O needed for printf
#include <stdio.h>
 
// Main function
int main()
{
  // The dummiest example
  printf("Hello World !\n");
 
  // always return something
  // 0 is success
  return 0;
}

Mettez ce bout de code dans un fichier que vous nommerez hello_world.c. Pour compiler nous pourrons utiliser le compilateur de notre choix, en général à l'école vous utiliserez gcc ou clang (je vous conseille clang pour ses messages d'erreurs plus intéressants.)

> ls
hello_world.c
> clang hello_world.c
> ls
a.out  hello_world.c

Sans option, presque tous les compilateurs Unix produiront une binaire appelé a.out, pour changer ça, il faut passer l'option -o suivi du nom que vous désirez. Mais nous ne nous arrêterons pas là: nous allons ajouter toutes les options que nous utiliserons tout le temps.

• -Wall activons tous les warning classiques.
• -Wextra activons tous les warning supplémentaires
• -Werror les warning deviennent des erreurs
• -std=c99 on fait du C99
• -O2 niveau 2 d'optimisation (déclenche plus de warning.)

Ce qui nous donne:

> rm a.out
> clang -Wall -Wextra -std=c99 -O2 hello_world.c -o hello_world
> ls
hello_world   hello_world.c

Choisir son compilateur: les deux compilateurs à votre disposition produisent (pour ce que nous avons à faire) des exécutables sensiblement équivalents et proposent les mêmes options. Par contre, leur façon d'afficher les erreurs est différente. Le plus simple est de tester: enlevez un point-virgule quelque part (où tout autre erreur simple), compilez … en général après le choix est simple !

Make et règles automatiques

La commande make est capable de produire un exécutable à partir d'un fichier C toute seule sans fichier Makefile:

> rm hell_world
> make hello_world
cc     hello_world.c   -o hello_world

C'est bien, mais il manque nos options et nous ne pouvons pas choisir le compilateur (cc correspond en général à un gcc, mais ce n'est pas toujours le cas.) Heureusement, cette règle automatique utilise des variables d’environnement que l'on peut régler pour obtenir ce que l'on souhaite.

Vous pouvez fixer ces variables dans votre shell ou les mettre dans un Makefile minimal. Nous choisirons la deuxième solution qui nous permettra également d'ajouter une règle pour faire le ménage (suppression des fichiers ~ d'emacs ou des fichiers .o par exemple.)

Voici un Makefile je vous invite à le lire attentivement.

# Makefile with basic concepts
 
# Define compiler and options
CC=clang
CFLAGS= -Wall -Wextra -std=c99 -O2
 
# avoid calling make without option
# ONLY FOR THIS EXERCICE
all:
	@echo "*** NO RULES ***"
	@false
 
clean::
	rm -f *~ *.o
 
# END (do not delete)

Quelques tests:

> rm -f hello_world
> make hello_world
clang -Wall -Wextra -std=c99 -O2    hello_world.c   -o hello_world
> make hello_world.o
clang -Wall -Wextra -std=c99 -O2   -c -o hello_world.o hello_world.c

La dernière commande nous montre que l'on peut produire des fichiers .o directement également.

Options, en-têtes, pages de manuel

Cette exercice à pour but de vous faire lire les pages de manuel pour trouver les en-têtes standard à ajouter pour faire marcher un programme.

Voici un programme dont ont été enlevées toutes les inclusions d'en-tête.

/* A little example with includes */
 
/*
 * Goals:
 * * understand include strategy
 * * read man pages for function
 */
 
 
// add here missing includes
 
const int LIMITS[] =
  {
    RLIMIT_CORE,
    RLIMIT_CPU,
    RLIMIT_DATA,
    RLIMIT_FSIZE,
    RLIMIT_NOFILE,
    RLIMIT_STACK,
    RLIMIT_AS
  };
 
const char *LIMIT_NAME[] =
  {
    "RLIMIT_CORE",
    "RLIMIT_CPU",
    "RLIMIT_DATA",
    "RLIMIT_FSIZE",
    "RLIMIT_NOFILE",
    "RLIMIT_STACK",
    "RLIMIT_AS"
  };
 
void print_limit(const char *name, const struct rlimit *rlp)
{
  printf("%s: ",name);
  if (rlp->rlim_cur == RLIM_INFINITY)
    printf("unlimited");
  else
    printf("%lu",rlp->rlim_cur);
  if (rlp->rlim_max == RLIM_INFINITY)
    printf(" unlimited\n");
  else
    printf(" %lu\n",rlp->rlim_cur);
}
 
int main()
{
  struct rlimit         rlp;
  printf("break address: %p\n", sbrk(0));
  for (size_t i=0; i < sizeof (LIMITS) / sizeof (int); ++i)
    {
      if (getrlimit(LIMITS[i], &rlp) < 0)
        {
          perror("getrlimit failed");
          return 2;
        }
      print_limit(LIMIT_NAME[i], &rlp);
    }
  return 0;
}

Vous devriez commencer par regarder les pages de manuel des fonctions qui apparaissent dans le programme (vous pouvez essayer de compiler, mais vous risquez d'avoir beaucoup d'erreur.)

Les fonctions à regarder sont (au minimum): getrlimit(3), printf(3) et sbrk(2) (dans l'ordre, la première page permet d'enlever beaucoup d'erreur.)

Ligne de commande

Voir le contenu

La ligne de commande d'un programme (les options que vous passez à celui-ci) se contrôle à l'aide des paramètres de la fonction main de votre programme.

int main(int argc, char *argv[])
{
  // do your job here
  // always return some int
  return 0;
}

Le paramètre argc est la taille du tableau d'arguments tandis que argv est (un tableau de chaînes de caractères) le tableau en question. Attention, le tableau d'argument contient toujours en case 0 le nom du programme. On en conclut donc que argc > 0 dans tous les cas et qu'il y a des arguments uniquement lorsque argc > 1.

Vous allez maintenant essayer d'écrire un programme qui affiche sa ligne de commande sous la forme suivante:

> ./args a b c d e
argv[0] = "./args"
argv[1] = "a"
argv[2] = "b"
argv[3] = "c"
argv[4] = "d"
argv[5] = "e"

Pour indication, la chaîne de format utiliser pour la fonction printf sera "argv[%d] = \"%s\"\n"

Un petit exemple d'usage

Dans la suite nous allons faire plusieurs fonctions arithmétiques, il faudrait pouvoir les tester facilement. Le but est donc d'utiliser les arguments sur la ligne de commande, s'ils sont présents, ou de fournir une valeur par défaut si ce n'est pas le cas.

• Écrire un programme qui affiche la somme (par défaut) de 20 et 22, s'il y a un argument (que l'on appellera x) le programme affichera x + 20 et enfin s'il y a deux arguments (x et y) le programme affichera x + y.

Exemple:

> ./simple
20 + 22 = 42
> ./simple 1
1 + 22 = 23
> ./simple 21 21
21 + 21 = 42

Vous aurez besoin de la fonction atoi(3) pour convertir les chaînes de caractères.

Arithmétique

Nous allons maintenant écrire une série de fonctions arithmétiques classiques. Vous regrouperez ces fonctions dans un unique fichier simple_math.c que nous utiliserons après dans un programme global.

Il est par ailleurs fortement conseillé de tester vos fonctions, pour ça inspirez vous de la dernière question sur la ligne de commande pour écrire une petit programme de test simple. Vous pouvez également utiliser assert(3) (lisez donc le bon manuel … )

Cette partie sera à rendre, vous devrez rassembler l'ensemble des fonctions suivantes dans un fichier nommé simple_math.c

Factorielle

On ne présente plus le classique des classiques, vous pouvez ici en faire une version récursive ou une version itérative.

/*
 * fact(n) compute n!
 * fact(0) returns 1
 */
unsigned fact(unsigned n);

Il n'est pas nécessaire de gérer les nombres négatifs, on travaille avec des nombres non-signés (unsigned) donc strictement positifs.

Fibonacci

Autre classique, on utilisera ici la version standard dans laquelle fibo(0) == 0,fibo(1) == 1 et fibo(n) = fibo(n-1) + fibo(n-2), vous pourrez biens sûr faire une version récursive ou une version itérative (voir les deux.)

/*
 * fibo(n) compute the n-th term of Fibonacci sequence
 * fibo(0) returns 0
 * fibo(1) returns 1
 */
unsigned fibo(unsigned n);

Puissance

Encore un autre classique: $a^b$ (avec a et b des entiers.)

Le but est bien sûr d'utiliser l'exponentiation rapide basée sur l'équation suivante: $a^{2\times n} = \left(a^2\right)^{n}$, je vous laisse chercher l'algorithme complet (essayez de faire une version itérative, c'est un bon exercice.)

/*
 * power(a, b) computes a power b
 */
unsigned power(unsigned a, unsigned b);

Le crible d'Eratosthene

Il s'agit maintenant d'afficher tous les nombres premier inférieurs à n (le paramètre de la fonction.)

Pour l'algorithme nous aurons besoin d'un tableau de n+1 cases (ce sera plus simple) indiquant (à la fin) si l'entier i est premier ou non. Au début de l'algorithme, tous les nombres sont considérés comme premier. Comme il n'y a pas de booléen en C, nous allons utiliser un tableau d'entiers non-signés sur 8 bits, que l'on créera comme suit:

  // n is our parameter
  uint8_t *prime;
  prime = malloc(n+1);

Ensuite, vous devez faire une boucle de i=2 à i=n (inclus), si i est marqué comme premier (dans le tableau prime) alors on l'affiche et on rentre dans la seconde boucle, sinon (i n'est pas premier) on passe au suivant. La seconde boucle va marquer tous les multiples de i comme n'étant pas premier.

Quelques remarques:

• En général, on arrête la boucle à $\sqrt n$ et on utilise le tableau de nombres premier (qui se trouve complètement remplis) mais ici on veut tous les afficher, donc autant le faire directement pendant la boucle principal et laisser celle-ci aller au bout du tableau.
• Pour marquer tous les multiples de i, on peut observer que:
  • tous les multiples inférieurs à $i^2$ sont déjà marqués
  • les autres multiples sont de la forme $i^2 + i*j$ avec j commençant à 0 et allant jusqu'à ce que i^2 + i*j atteigne ou dépasse n.

Pour l'affichage, dans un premier temps vous pouvez vous contenter d'afficher une nombre par ligne. Puis essayer d'obtenir quelque chose comme ça:

002 003 005 007 011 013 017 019 023 029 031 037 041 043 047 053 059 061 067 
071 073 079 083 089 097 101 103 107 109 113 127 131 137 139 149 151 157 163 
167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 
271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 
389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499

Pour ça, il faut utiliser l'alignement de printf(3) ainsi que la valeur de retour (toujours de printf(3)) pour savoir quand passer à la ligne.

// prime(n) print all prime number between 2 and n
void prime(unsigned n);

Calcule de racine carrée

Pour commencer, nous allons calculer la partie entière de la racine carrée. Pour ça nous allons utiliser la méthode de Héron (qui est un cas particulier de la méthode de Newton.)

Il s'agit d'un algo qui travaille par approximations successives. Soit x l'approximation courante pendant le calcule de $\sqrt n$, on supposera (et on fera en sorte que ce soit vrai) que 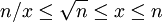$n/x \leq \sqrt n \leq x \leq n$. Comme notre approximation est plus grande que la racine, on a l'inéquation suivante: $n/x \leq \sqrt n \leq x$.

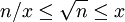On va resserrer l'intervalle entre x et n/x pour se rapprocher de la racine. Le meilleur candidat pour se rapprocher de la bonne valeur sera la moyenne entre x et n/x. Pour la partie entière de la racine, on aura le bon résultat dès que x <= n/x (lorsque les bornes de l'intervalle se croisent.)La valeur initiale de l'approximation (tant qu'elle respecte les conditions) n'a pas d'impacte sur le résultat, on prendra donc n. Un choix plus intelligent permet par contre d'améliorer les performances. On prendra soin de ne pas calculer avec cette méthode la racine de 0 ou de 1.

Implémenter la fonction racine:

/*
 * integer_sqrt(n) returns the integer part of the square root of n.
 */
unsigned integer_sqrt(unsigned n);

Vous pouvez tester votre fonction de deux façons:

• en produisant une série de valeurs entières aléatoire n et vérifiant que integer_sqrt(n*n) == n
• en produisant une série de valeurs entières aléatoire n et en vérifiant que x * x <= n && n < (x + 1) * (x + 1) avec x = integer_sqrt(n)

Nous allons maintenant effectuer le même calcule sur les floattants. L'algorithme est le même, mais cette fois-ci, on relâchera la contrainte sur la position relative de l'approximation (elle peut donc être plus petite que la racine) et en arrêtant le calcule lorsque la distance entre x et n/x est inférieure à un seuil arbitraire (on prendra 1e-6.)

Pour écrire votre fonction, vous pourriez trouver pratique de disposer d'une fonction min sur les flottants. Cette fonction sera implémentée avec l'attribut static inline.

static inline
double dmin(double a, double b) { return a<b?a:b; }

À vous de jouer !

/*
 * double_sqrt(n) Compute the square root of n
 */
double double_sqrt(unsigned n);

Il est évident que vous ne devez pas utiliser la fonction sqrt(3) de la libc, mais par contre, vous aurez peut être besoin de fonction comme abs(3) qui se trouve dans math.h. Attention, à la compilation vous aurez besoin de vous lier à la bibliothèque m, regarder le Makefile fourni à la fin du sujet (dans la partie Rendu.)

Tout rassembler

Pour finir, nous allons regrouper les fonctions précédentes dans un seul programme. Nous utiliserons la ligne de commande pour choisir la fonction à tester et lui passer les paramètres attendus.

Plusieurs fichiers

Nous avons regroupé nos fonctions dans un fichier simple_math.c, il nous faut maintenant un fichier d'en-tête pour ce fichier: simple_math.h

La première chose à faire est de rassembler toutes les déclarations de fonctions (les prototypes donnés dans le sujet) dans le fichier simple_math.h.

Maintenant, il faut protéger (même si dans notre cas ce n'est pas vraiment nécessaire) l'en-tête en suivant les recommandations officiels: un marquage via le pré-processeur. Voici le schéma à suivre, il faut d'abord trouver un nom pour le marqueur, dans notre cas, on choisira _SIMPLE_MATH_H_ (c'est la méthode habituelle), pour la suite voila la marche à suivre:

#ifndef SIMPLE_MATH_H_
#define SIMPLE_MATH_H_
 
/* Prototypes go here */
 
#endif

Lorsqu'il faudra compiler le programme final, vous aurez besoin de compiler le fichier simple_math.c pour obtenir simple_math.o (make sait le faire pour vous !)

Le programme principal

Notre objectif est maintenant d'écrire un programme principal qui à partir d'option sur la ligne de commande va sélectionner la fonction à appeler. On va faire un truc simple, le premier paramètre sera un entier que l'on fera correspondre avec la fonction à appeler. Les autres paramètres serviront comme arguments aux fonctions.

Comme indiquer dans le tableau suivant, les paramètres autres que le premier sont optionnels et les valeurs par défaut sont indiqués dans le tableau.

0	fact	Un seul paramètre, valeur par défaut 5
1	fibo	Un seul paramètre, valeur par défaut 7
2	power	Deux paramètres, valeurs par défaut 2 et 16
3	prime	Un seul paramètre, valeur par défaut 500
4	sqrt	Un seul paramète, valeur par défaut 200
5	double_sqrt	Un seul paramète, valeur par défaut 200

Inspirez vous des exercices précédents pour gérer les valeurs par défaut.

S'il n'y a aucun paramètre vous devez quitter le programme courant avec un message d'erreur de votre choix et la valeur de sortie (valeur de retour de la fonction main) de 1.

S'il y a au moins un paramètre mais que celui-ci ne correspond à aucune fonction, vous devez quitter le programme avec un message d'erreur de votre choix et la valeur de sortie 2.

Fichiers

• Makefile
• simple_math.c
• simple_math.h
• main.c

# Simple Makefile
# Practical session 01
 
# Global Compilation Variables
 
# The compiler
CC=clang
 
# Pre-processor flags
CPPFLAGS=
 
# C compiler flags
CFLAGS= -Wall -Wextra -Werror -std=c99 -O3
 
# Linker flags
LDFLAGS=
 
# Linker libs
LDLIBS= -lm
 
# all target just call the production of main
all: main
 
# main target using implicit rules, just express dependencies
main: main.o simple_math.o
 
# clean compilation products
clean:
	rm -f *~ *.o
	rm main
 
# END of File