20131112:TP:OCaml:Imperatif:Avance:Memoization
Sommaire
Introduction
La mémoïzation est une technique d'optimisation qui consiste à conserver les résultats d'une opération d'un appel à l'autre. L'objectif est donc d'accumuler les résultats déjà établis dans une structure (impérative) pour éviter de les recalculer au besoin.
On utilise souvent la mémoïzation sur des structures construites par saturation ou fermeture transitive: lorsque l'appartenance à la structure est définie à l'aide d'une relation initiale et d'une définition récursive.
- Pour ce TP vous devrez lire (en partie du moins) la documentation des modules Hashtbl[1] et Set[2] (notamment les détails sur le foncteur Set.Make.)
Préparation: variables statiques en OCaml
L'un des points importants que nous allons utiliser dans la suite est la possibilité de créer une valeur locale qui persiste d'appel en appel. En cours nous avons vu l'exemple suivant:
let (next,reset) = let r = ref 0 in ( (fun () -> incr r; !r), (fun () -> r := 0) )
On peut utiliser cette technique pour créer un dictionnaire accompagné d'une fonction d'ajout et d'une fonction de recherche. Le but est toujours de ne pas avoir le conteneur visible comme une variable globale. Pour ça nous allons utiliser une table de Hash (fournie par le module Hashtbl.) Les opérations du module dont nous auront besoin sont les suivantes:
(* Hashtbl.create n build a new hash table with initial size n*) val create : int -> ('a, 'b) t (* Hashtbl.add t k v add the association (k,v) to the table t *) val add : ('a, 'b) t -> 'a -> 'b -> unit (* Hashtbl.find t k look for the first pair (k,v) in table t and return v or raise Not_found *) val find : ('a, 'b) t -> 'a -> 'b
- Exercice: sur le même modèle que le couple de fonction (next,reset), créer un couple de fonction (add_dico,find_dico) qui permet d'ajouter et de supprimer dans un dictionnaire statique caché (une table de Hash.)
Vous pourrez tester vos fonctions avec le code suivant:
let (add_dico, find_dico) = (* FIX ME *) let base = [ ("feuille","leaf"); ("arbre","tree"); ("noeud","node"); ("sommet","vertice"); ("arc","edge"); ] let find_print w = try Printf.printf "%s: %s\n" w (find_dico w) with | Not_found -> Printf.printf "%s: pas de traduction.\n" w let main () = begin List.iter (fun (k,v) -> add_dico k v) base; List.iter find_print ["feuille";"arc";"arête";"noeud";"nœud";"arbre"]; exit 0 end let _ = main ()
Mémoïzation Simple
Commençons par des choses simples. Toutes fonctions peut être mémoïzée (même si ce n'est peut être pas forcément pertinent.) On va donc essayer avec des exemples simples.
Voici un exemple de fonction calculant une racine carrée:
let int_sqrt n = let r = ref n in let r' = ref (n+1) in while !r' > !r do r' := !r; r := (!r + n/(!r))/2; done; !r'
- Modifier cette fonction pour intégrer une table statique des valeurs déjà calculées.
Mémoïzation d'une fonction récursive
Si on applique la même méthode pour une fonction récursive, on profite bien évidement de la même optimisation, mais pour être sûr que la fonction profite réellement de la mémoïzation, il faut utiliser la table de valeur à chaque appel de la fonction récursive.
Voici un implementation particulière de la suite de Fibonacci, où l'on récupère en plus du résultat attendu un dénombrement des appels récursifs:
let rec fibo count = function | (0|1) as x -> x | n -> incr count; fibo count (n-1) + fibo count (n-2)
Voici un exemple d'utilisation (avec l’interpréteur):
# let count = ref 0;;
val count : int ref = {contents = 0}
# fibo count 5;;
- : int = 5
# !count;;
- : int = 7
# count := 0;;
- : unit = ()
# fibo count 10;;
- : int = 55
# !count;;
- : int = 88
- Modifier la fonction fibo précédente pour utiliser une table de valeur (mémoïzation)
Comparer le nombre d'appels récursifs entre les deux versions. Voici un example comparable au précédant:
# let count = ref 0;;
val count : int ref = {contents = 0}
# fibo count 5;;
- : int = 5
# !count;;
- : int = 6
# count := 0;;
- : unit = ()
# fibo count 5;;
- : int = 5
# !count;;
- : int = 1
# count := 0;;
- : unit = ()
# fibo count 10;;
- : int = 55
# !count;;
- : int = 11
- Note: pensez à séparer la fonction récursive de la création de la table de valeurs à l'aide d'une fonction auxiliaire. Vous devez notamment gérer les cas d'arrêts classiques (1 et 0), le cas d'arrêt lorsque la table de valeur contient une réponse pour la valeur recherchée et enfin le cas récursif dont vous prendrez bien soin d'ajouter le résultat à la table avant de le renvoyer.
Mémoïzation généralisée d'une fonction récursive
Comme toute fonction pure peut être mémoïzée, à l'aide de l'ordre supérieur et des tables de hash prédéfinies, on obtient facilement une fonction de mémoïzation générique:
let memo f = let h = Hashtbl.create 101 in (* on choisit un nombre premier adéquate *) fun x -> try Hashtbl.find h x with Not_found -> let y = f x in Hashtbl.add h x y; y
Cette fonction est un générateur de fonction, on devra l'appliquer à la fonction à mémoizer pour obtenir la version efficace avec sa table associée.
let ma_fonction x = (* fonction lourde à calculer *) (* version avec mémoïzation *) let ma_fonction_rapide = memo ma_fonction
Seulement, sur une fonction récursive, on ne profite pas de la mémoïzation lors du calcul de la fonction récursive. Il nous faut donc écrire un opérateur de point fixe (une fonction qui simule le calcul récursif.)
Pour ça, il faut passer par une forme particulière de récursivité: la continuation. Il s'agit ici d'une variante simple de cette technique (qui nécessite normalement un support particulier dans le langage.) Le principe est le suivant, la fonction récursive par continuation prend en paramètre la fonction permettant de faire la suite du travail.
Voici un exemple avec factorielle:
(* opérateur de point fixe *) let mu f = let rec aux x = f aux x in aux (* factorielle par contination *) let cont_fact fact = function 0|1 -> 1 | n -> n * fact (n-1) (* application *) let x = mu cont_fact 5
Bien évidement, ce principe n'a que peut d'intéret dans l'exemple courrant. Mais, combiner avec les techniques de mémoïzation, il nous permet d'appliquer la mémoïzation aux fonctions récursives.
- Exercice: écrire une version de la fonction memo sur le même principe que la fonction mu.
val memo : (('a -> 'b) -> 'a -> 'b) -> 'a -> 'b
Appliquer à la version suivante de Fibonacci, on obtient un calcul de fibonacci presque linéaire (pour les premières éxécutions) et qui tend vers du temps constant après de nombreuses utilisation.
let cont_fibo next = function | 0 | 1 as x -> x | x -> next (x-1) + next (x-2) let fibo = memo cont_fibo
Vous pouvez évaluer l'efficacité de notre mémoïzation en ajoutant dans votre fonction de mémoïzation un affichage à chaque fois que la valeur demandée n'est pas dans la table de hash.
Mémoïzation avancée: relation transitive
Cloture transitive
Une relation transitive est une application dans un ensemble dans lui même, définie à l'aide d'une relation initiale (le noyeau de notre relation) et d'une définition récursive. Supposons que 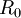
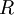
La relation 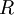
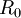
Utilisation de la mémoïzation
En fonction de la nature de 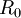
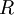
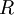
On va donc représenter notre relation à l'aide d'une structure modifiable nous permettant de sauver les résultats intermédiaires.
Il existe deux possibilités pour stocker la relation: stocker les couples qui lui appartiennent ou choisir de stocker les couples sous forme d'association entre un élément et tous ceux avec qui il est relié. Cette deuxième solution est la plus adaptée à notre problème.
Construction des relations
Les relations que nous allons construire contiendront des couples de string.
Pour notre relation, nous avons besoin de deux choses: la structure globale contenant l'association entre une clef et les élément qui lui sont associés, et justement l'ensemble des éléments associés à une clef. Pour le second, nous choisirons d'utiliser le module Set d'OCaml, pour ça il nous faut construire une version pour les chaînes de caractères:
module StringSet = Set.Make(String)
Une relation sera représentée à l'aide d'une table de Hash, nous utiliserons la fonction suivante pour récupérer l'ensemble des éléments en relation avec un autre:
let get_succ x r = try Hashtbl.find r x with Not_found -> StringSet.empty
Ensuite, nous utiliserons pour la mise à jour de la relation la fonction suivante:
let extend r a b = Hashtbl.replace r a (StringSet.add x (get_succ a r))
Pour constuire notre table de hash, il nous faut une taille de départ, en général, on choisit une valeur de même ordre de grandeur que la taille des données à stocker. On choisit également un nombre premier pour miniser les collisions. Nous allons commencer par écrire une petite fonction qui trouve le prochain nombre premier depuis un entier donné.
- Exercice: écrire la fonction suivante:
val next_prime: int -> int
- next_prime n renvoie le plus petit nombre premier supérieur ou égal à n
- Exercice: écrire la fonction suivante
val make : ('a * StringSet.elt) list -> ('a, StringSet.t) Hashtbl.t
- make [(a1,b1); ...; (an,bn)] construit une relation à partir de la liste de couple en paramètre.
- Exercice: écrire la fonction suivante
val print_rel : (string, StringSet.t) Hashtbl.t -> unit
- print_rel r affiche une relation sur la sortie standard sous la forme:
d : [ a; b; ] a : [ b; ] b : [ c; ] c : [ d; ]
- Note: utilisez les fonctions Hashtbl.iter, StringSet.iter et Printf.printf.
Relation transitive sans mémoïzation
Dans un premier temps, nous allons construire la fonction correspondant à notre relation transitive sans mémoïzation.
L'algorithme est simple: soit (a,b) est dans le noyau de la relation (les couples stockés), soit il existe un c tel que (a,c) est dans le noyau (c appartient aux successeurs de a) et (c,b) appartient à la relation.
On a une simple définition récursive, il suffit de traduire tout ça en OCaml. Pour ça, nous avons à notre disposition les opérations suivantes: StringSet.mem x s (vrai si x appartient à s), StringSet.exists f s (renvoie vrai s'il existe un élément x de s, tel que f x renvoie vrai.)
L'algorithme le plus approprié ici correspondra à une forme de parcours en profondeur (notre relation est en fait un graphe !), nous choisirons la profondeur (qui peut également être vu comme un algorithme avec backtracking) car c'est l'algorithme qui nous permettra de stocker le plus de résultats intermédiaires dans la version avec mémoïzation (et donc celui qui sera, à terme, le plus performant.)
Attention, dans ce type de parcours (nous sommes pas dans un arbre) il faut faire attention aux circuits: en effet, prennons le noyau de relation suivante 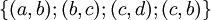
Au final, l'algorithme ressemble à:
is_in a b r:
- renvoie vrai si b est dans get_succ a r
- sinon: on parcours l'ensemble des successeurs c de a:
- si c est marqué on continue sur le suivant
- sinon, on marque c, et on teste si is_in c b r, si c'est le cas on renvoie vrai, sinon on continue sur le suivant.
Pour garder les éléments marqués, on utilisera un ensemble du module StringSet et pour continuer sur le suivant si le résultat est faux, on s'appuiera sur la fonction StringSet.exists.
- Exercice: écrire la fonction suivante:
val is_in : StringSet.elt -> StringSet.elt -> (StringSet.elt, StringSet.t) Hashtbl.t -> bool
- is_in a b r renvoie vrai si (a,b) est dans la relation transitive dont le noyau est r.
Avec mémoïzation
On va maintenant modifier (enfin, réécrire, pour pouvoir les comparer) la fonction qui teste l'appartenance à la relation. Mais cette fois-ci, on va stocker les résultats intermédiaires dans le noyau de la relation. On étendra la relation (avec extend) lorsque:
- is_in a b r renvoie vrai et que b n'est pas successeur de a
- pour toutes les valeurs intermédiaires, c, rencontrées on étendra la relation en ajoutant c aux successeurx de a.
- Exercice: écrire la fonction suivante:
val is_in_memo : StringSet.elt -> StringSet.elt -> (StringSet.elt, StringSet.t) Hashtbl.t -> bool
- Astuce: lorsque l'on veut renvoyer un booléen et faire une action si celui-ci est vrai, on peut se passer de if ... then ... en j
ouant avec l'opérateur &&:
let test_affiche printer f x = f x && (printer x ; true)
- si f x renvoie vrai, alors le deuxième membre (qui renvoie toujours vrai) est évalué (et l'affichage a lieu) sinon, l'affichage n'a pas lieu.
Tester !
Pour tester, voici une fonction qui lit dans un channel d'entrée ligne par ligne des couples de string. Le format est simple sur chaque ligne nous avons deux string séparées par un espace (qui doit être le seul espace de la ligne.)
let read_pair cin = let l = input_line cin in let p = String.index l ' ' in (String.sub l 0 p, String.sub l (p+1) ((String.length l) - (p+1))) let rec from_file cin = try let p = read_pair cin in p :: from_file cin with _ -> []
Vous pouvez utiliser cette fonction sur l'entrée standard (stdin) ou sur un fichier ouvert avec open_in. De plus, la fonction read_pair peut également servir pour lire des paires à tester.
Un exemple de fichier possible en entrée:
a b a g b c c d d e f a g h h i i j j k b g k f e l l b
Pour finir, regrouper l'ensemble du code et écrivez une fonction main qui construit la relation d'origine via from_file et make et tester quelques couples avec les deux fonctions.
Pour bien voir la différence entre la version avec mémoïzation et sans, il faut:
- tester plusieurs couples d'affiler
- afficher le nombre de valeurs marquées (le nombre d'élément dans un ensemble est disponible avec StringSet.cardinal)
Normalement, la première recherche sera identique dans les deux cas, après la version avec mémoïzation devrait tester de moins en moins de valeurs.
Vous pouvez également afficher la relation après la recherche pour voir les éléments ajoutés à chaque fois.